The optimal quantity of CBDC in the euro area

Early evidence from an event study suggests that the expected impact of issuing a digital euro on bank profitability and lending depends on the bank’s reliance on deposit funding and the amount of digital euro in circulation. This is due to a perceived degree of substitutability between central bank digital currencies (CBDCs) and bank deposits, which in normal times are a relatively cheap form of bank funding. In this SUERF policy note we use a macro-banking DSGE model calibrated to quarterly data of the euro area economy to investigate optimal CBDC rules. According to our analysis, the optimal amount of CBDC in circulation for the case of the euro area lies between 15% and 45% of quarterly GDP. Optimal CBDC rules are effective in mitigating the risk of bank disintermediation and induce significant welfare gains. 

In recent years, the use of cash for transactions has significantly declined, while the demand for digital means of payment for retail purposes has steadily increased (Auer et al. 2020). In response, central banks have started to investigate the implications of issuing central bank digital currencies (CBDCs). One of the important challenges of issuing a CBDC is the risk of bank disintermediation through deposit substitution (Carapella and Flemming 2020; Niepelt 2021). Much of the current policy debate focuses on how to calibrate the amount of CBDC in circulation to ensure that the potential benefits of CBDC materialize without harming monetary and financial stability through bank disintermediation (Bindseil and Panetta 2020; Jamet et al. 2022). One challenge in this regard is that advanced economies have no experience with CBDCs and, hence, there is no available data on which empirical analysis can be performed. For this reason, the literature has focused mainly on studying the implications of CBDCs within theoretical models.

In this SUERF policy note, we present some novel empirical evidence on the expected impact of CBDC on bank profitability and lending behavior and report on the development of a quantitative DSGE model that allows us to investigate the relevant trade-offs. The findings underscore the importance of adequately calibrating the amount of CBDC in circulation.1

Evidence: The impact of digital euro news on bank stock prices and lending behaviour

Early empirical evidence on the impact of digital euro news on bank stock prices and lending behaviour suggests that market participants perceive a certain degree of substitutability between deposits and CBDC and that the extent to which this may have a bearing on banks’ lending conditions depends on their reliance on deposit funding and the design of the CBDC.

The response of bank valuations to news about the digital euro project provides insights as to what market participants expect the effect of a digital euro on bank profitability to be. Figure 1 shows the cumulated impact of digital euro news on abnormal returns on euro area banks’ stock prices. Banks’ valuation decreased after the ECB stated its intention to intensify work on a digital euro in early October 2020 (ECB 2020a; ECB 2020b).2 The drop was concentrated among banks with a higher reliance on deposit funding, and was later reabsorbed in early February 2021 when potential limits on individual holdings and other qualifications about the digital euro project that may mitigate deposit substitution were conveyed to the public.3

The reaction of stock prices may have conveyed information about the impact that the digital euro project may have on the business model of banks that rely heavily on deposit funding. Moreover, an adverse assessment by market participants as to the prospects of a given bank in a world with a digital euro may have also directly translated into more expensive market-based funding options for that bank, ultimately exerting pressure on bank lending conditions. Developments in corporate loan markets measured with transaction level data from AnaCredit (the European credit register) suggest that one percentage point drop in stock market returns attributable to digital euro news was associated with a decrease in loan volumes of over 0.3% (Figure 2). Consistent with the recovery of stock market returns observed since early February 2021, the impact on lending disappeared following the discussion of possibly restricting the amount of CBDC in circulation.

Figure 1: Stock market reactions to CBDC news by euro area banks (percentage points)

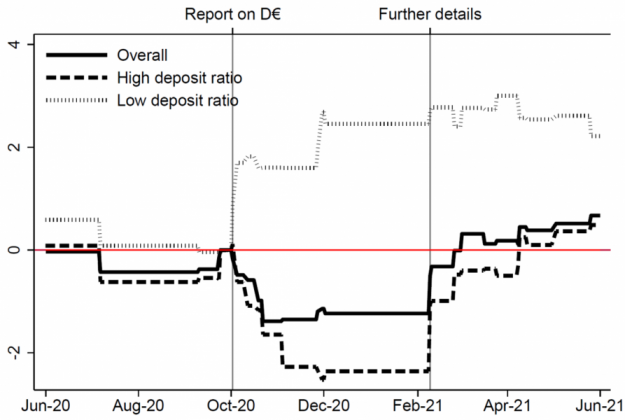
Sources: Burlon, Montes-Galdón, Muñoz and Smets (2022). Notes: A 3-factor Fama-French model is fitted to two-day stock market returns of euro area banks, isolating the abnormal returns occurred at key events for each bank. Each horizontal segment reports the cumulated abnormal returns up to the latest key event, relative to the level on 1 October 2020. The solid line reports the average across all banks in the sample. The dashed and dotted lines report the average within two groups of banks, those with deposit ratio above or below the median, respectively. The two grey vertical lines indicate the publication of the ECB report on a digital euro on 2 October 2020 and of further details about the project on 9-10 February 2021. 

Figure 2: Predicted change in loan volumes to firms associated with a negative reaction of bank stock prices to CBDC news (percentages of volumes in October 2020) 

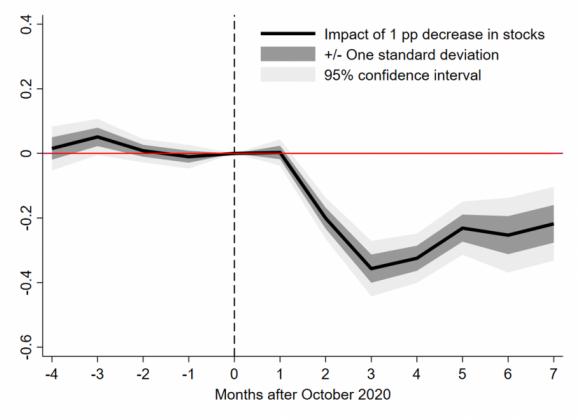
Sources: Burlon, Montes-Galdón, Muñoz and Smets (2022). Notes: In each month, the growth in lending volume at the bank-firm level since October 2020 is regressed on the bank-level exposure to abnormal returns up to end-October 2020. Firm effects control for demand factors. The solid line reports, for each monthly horizon from October 2020 indicated on the horizontal axis, the impact of 1 pp decrease in (cumulated) abnormal returns in October 2020. Shaded areas represent confidence intervals based on standard errors clustered at the bank level. 

A quantitative macro-banking DSGE model for CBDC analysis: Key features and transmission

Against this background, we develop a macro-banking DSGE model with some distinctive features. First, it captures the main transmission channels through which the introduction of CBDC could affect the banking sector and the real economy. Second, the model is calibrated to quarterly data of the euro area for the period 2000:I – 2021:II, and matches a number of first and second moments from banking and macroeconomic aggregates. Third, it is well suited for policy and welfare analysis, which allows us to investigate a variety of CBDC policy rules and give a sensible range of values for the optimal amount of CBDC in circulation.

The monetary economy we model features two types of households: patient households (i.e., savers) who hold a variety of financial and monetary instruments, three of which provide them with liquidity services (i.e. bank deposits, cash and CBDC), and impatient households (i.e., borrowers) who borrow funds from banks against housing collateral (Iacoviello 2005). Savers own all firms operating in the economy: Each non-financial corporation (NFC) is run by a manager, who obtains bank lending against the firm’s capital, and a retailer (intermediate good producer) who operates under monopolistic competition in the market of her own variety and sets prices a la Calvo (1983). Banks intermediate funds by borrowing from savers (in the form of deposits) and lending to impatient households and NFCs (in the form of loans). Banks’ assets (i.e., loans, government bonds and reserves) are funded by equity, deposits and central bank borrowing. Banks operate subject to capital and liquidity (reserves) requirements and obtain complementary funding from the central bank against eligible collateral (i.e., government bonds).4 The government finances its deficit by issuing government bonds. Tax revenues, collected in a lump-sum fashion from households, are adjusted in response to changes in the holdings of government debt by banks and patient households. The central bank sets the lending facility rate according to a simple Taylor-type rule and the interest rate on reserves to maintain a constant corridor between these two policy rates. Central bank assets (i.e., loans to private banks) are financed by issuing reserves, banknotes and CBDC and its profits are transferred to the government. CBDC policy is characterized either by a simple CBDC quantity rule that sets the supply of CBDC provided by the central bank or by an interest rate rule that determines the interest rate on CBDC.

The model captures the following transmission channels of the issuance of CBDC to the economy. Due to the imperfect substitutability between the three assets that provide liquidity services, an increase in the amount of CBDC in circulation is associated with a decline in savers’ holdings of cash and deposits.5 In response, banks reduce their holdings of reserves in line with the reserve requirement. This has two main consequences for the accounts of the central bank. First, its balance sheet expands as the issuance of CBDC is not fully offset by the aggregate decrease in reserves and cash. Second, central bank profits soar due to an increase in its assets and a shift towards less costly liabilities, as under our calibration the equilibrium interest rate on CBDC will be lower than on cash or reserves. The increase in seigniorage relaxes the government budget constraint and puts downward pressure on taxes, thereby promoting private consumption, economic activity and bank lending. We call this the fiscal expansion effect of issuing CBDC. On the banks’ balance sheet, there is a reallocation of bank liabilities from deposits towards central bank funding and of bank assets from loans to the private sector towards government bonds. The latter is due to an increased demand for government bonds as collateral for borrowing from the central bank. As a consequence, bank lending margins compress, which tends to adversely affect bank lending supply and real GDP. We call this the bank disintermediation effect of issuing CBDC. Note that the negative effect on bank interest rate margins may be reversed under a negative interest rate policy (on reserves) if there is a zero lower bound on deposits. However, under our calibration that captures a new normal with positive interest rates, the bank disintermediation effect of a permanent issuing CBDC is larger than the fiscal expansion effect.

Welfare analysis: Optimal CBDC policy rules and bank intermediation

Using this calibrated model we then perform welfare analysis considering six different CBDC policy rules. Three of those are quantity rules that specify the supply of CBDC as a fraction, ϕ_Y, of quarterly real GDP: (i) CBDC supply is a constant proportion of actual real GDP (procyclical rule); (ii) CBDC supply is a constant fraction of steady state real GDP (static rule); and (iii) CBDC quantity is a time-varying proportion of real GDP as it responds in a countercyclical fashion to changes in the output gap (countercyclical rule). Figure 3 plots the welfare effects of issuing different amounts of CBDC under the three policy regimes.6 Welfare implications and trade-offs are driven by three main effects: (i) a liquidity services effect according to which savers (i.e., CBDC holders) benefit from the availability of a monetary instrument that provides them with liquidity services and for which there is no perfect substitute in the economy; (ii) a bank disintermediation effect by which the deposit substitution of issuing CBDC leads to a compression in banks’ net interest margins which adversely affects lending supply and, thus, borrowers’ welfare; and (iii) a stabilization effect according to which the issuance of CBDC exerts a smoothing effect on bank lending and real GDP by stabilizing deposit holdings that positively affects borrowers’ welfare. Similar conclusions are reached for the case of three interest rate rules that link the interest rate on CBDC holdings to the deposit facility rate of the central bank.7

Figure 3: Welfare effects of CBDC quantity rules (welfare effects of ceteris paribus changes in ϕ_Y)

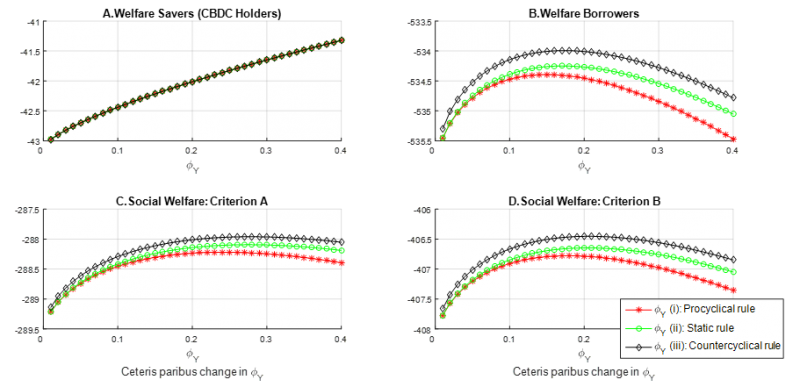
Sources: Burlon, Montes-Galdón, Muñoz and Smets (2022). Notes: Second-order approximation to the unconditional welfare of savers and borrowers as well as to the unconditional social welfare under welfare criteria “A” and “B” as a function of CBDC policy parameter ϕ_Y. The starred line, the dotted line, and the diamond line relate to CBDC quantity rules (i), (ii) and (iii), respectively.

Figure 4: Liquidity services, bank disintermediation and stabilization effects 

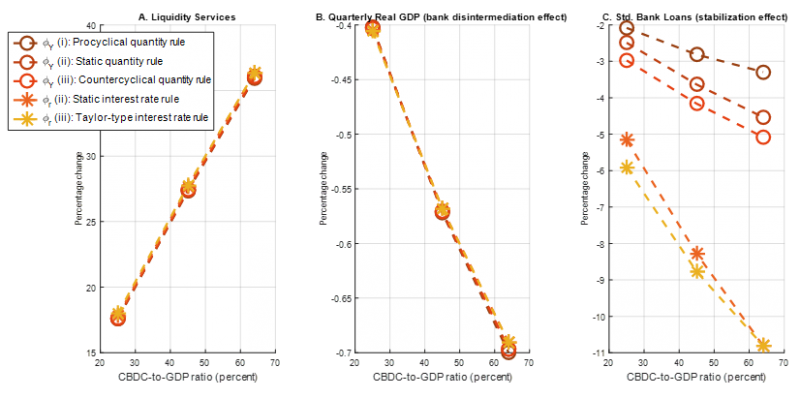
Sources: Burlon, Montes-Galdón, Muñoz and Smets (2022). Notes: For CBDC quantity rules of type (i), (ii) and (iii) and interest rate rules within the class (ii) and (iii), the figure reports the percentage change in the second-order approximation to the stochastic mean of liquidity services (panel A), the stochastic mean of quarterly real GDP (panel B), and the stochastic standard deviation of bank lending (panel C) arising when the economy moves from the no CBDC scenario to alternative CBDC scenarios under which the quantity of CBDC in equilibrium is assumed to be equal to 25%, 45% and 64% of quarterly real GDP, respectively. 

Figure 5: Steady state effects of CBDC policy rules 

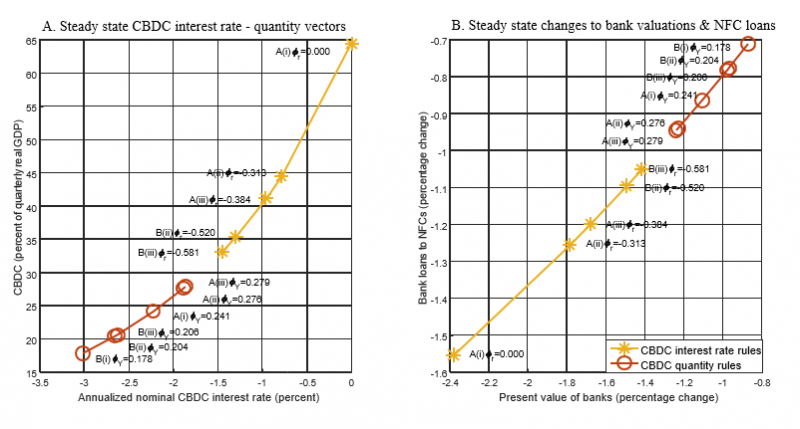
Sources: Burlon, Montes-Galdón, Muñoz and Smets (2022). Notes: For each of the six considered specifications of the CBDC policy rule and for welfare weighting criteria “A” and “B”, panel A reports the annualized nominal CBDC interest rate and the CBDC-to-real GDP ratio associated to each welfare-maximizing CBDC policy rule. For the same optimal policy rules, panel B displays the steady state impact on bank valuations and aggregate bank loans to firms. Bank valuations in the model are proxied by the recursive value of the representative bank (i.e., the objective function of banks’ optimization problem).

Figure 4 illustrates the magnitude of these three main effects by displaying the percentage changes in the second-order approximation to the stochastic mean of liquidity services (panel A), the stochastic mean of quarterly real GDP (panel B), and the stochastic standard deviation of bank lending (panel C) triggered by the introduction of a CBDC under different levels of central bank digital currency issuance in steady state. Our analysis reveals that the stabilization effect is the main factor explaining differences in terms of attainable welfare gains across different CBDC rules. In particular, a CBDC rule that implies a countercyclical provision of CBDC to the economy allows to better stabilize the economy.

For each of the six CBDC policy regimes and the two considered welfare weighting criteria, figure 5 shows the steady state CBDC interest rate – quantity vector (panel A) and the steady state impact on banks’ present value and lending to NFCs (panel B). Three findings are worth noting as they are relevant for the current policy debate and are consistent with the empirical evidence presented above. First, as discussed before there is a negative correlation between the amount of CBDC in circulation and banks’ valuations and lending to firms. CBDC rules that features a larger optimal supply of CBDC in steady state imply somewhat larger negative effects on bank valuations and lending. Second, depending on the CBDC quantity rule considered, the optimal quantity of CBDC in equilibrium lies between 15% and 45% of quarterly real GDP. In early February 2021, ECB Board member Panetta made a statement on the possibility of adopting a limit on individual CBDC holdings of EUR 3,000 which led to a trend reversal in the estimated impact of digital euro news on bank valuations and lending to firms (see figures 1 and 2). If all citizens in the euro area were to hold this maximum individual level of CBDC in 2021, the amount of CBDC in circulation would be roughly 34% of quarterly GDP.8 By way of contrast, if CBDC were to be supplied under no quantity limits and no remuneration (i.e., unlimited supply at a zero CBDC interest rate), the optimal amount of CBDC in circulation would be around 65% of quarterly GDP and the steady state effects on banks’ valuations and lending would be more sizable.

Third, the optimal amount of CBDC in circulation and, consequently, the impact on bank valuations and lending is larger under optimal interest rate rules than under optimal quantity rules. The relatively larger positive stabilization effect triggered by the countercyclical issuance of CBDC under optimal interest rate rules offsets the more negative bank disintermediation effect, leading to higher welfare gains attained by both savers (i.e., CBDC holders) and borrowers.9

Concluding remarks

To the extent that a certain degree of substitutability between CBDC and deposits is expected, the impact of CBDC on the banking sector depends on banks’ reliance on deposit funding and restrictions on the amount of CBDC in circulation. Our analysis shows that adequately calibrating the latter by means of optimal CBDC policy rules can mitigate the risk of bank disintermediation and induce significant welfare gains.