A primer on optimal policy projections

Abstract
Optimal policy projections (OPPs) offer a flexible way to derive scenario-based recommendations for monetary policymakers. Based on a recent Technical Paper (Dengler et al., 2024), this Policy Brief offers an introduction to OPPs, explaining the idea of the approach and illustrating it by means of different examples and applications.

Motivation

Between July 2022 and September 2023, the Governing Council (GC) of the European Central Bank (ECB) raised its interest rates by cumulative 4.5 percentage points, responding to the inflationary developments that followed the COVID-19 pandemic, the Russian invasion of Ukraine and the macroeconomic policies taken to cope with them. Unprecedented inflation rates experienced in the euro area during that time commanded a decisive response to deliver on the Eurosystem’s primary mandate of price stability. Yet, the GC faced – and still faces – the difficult task of bringing inflation to its target of 2 percent in the medium term without causing unnecessary harm to the real economy or to financial stability.

In doing so, the GC generally follows a measured approach, which takes into account all relevant information available at its respective meetings. An important piece of information is the medium-term outlook for inflation, output and other macroeconomic variables of interest, as given by Eurosystem staff projections. These projections paint a picture of how the economy would evolve if the GC were to set its instruments in the future as expected by financial markets. The GC then has to assess whether this projected evolution is in line with the Eurosystem’s mandate and if not, how to best set its instruments to make sure it is.

Optimal policy projections (OPPs) can serve as a useful input for the GC’s decision-making process by formalising and quantifying these trade-offs. They provide a reference point for discussions about the appropriate monetary policy stance. Using staff projections as a baseline scenario, OPPs deliver model-based time paths for the GC’s policy instruments that optimise a given objective function, taking into account how deviations of the policy instruments from market expectations would affect the economy.

Based on Dengler et al. (2024), this Policy Brief describes the OPP approach in intuitive terms and illustrates its versatility with two applications.

The OPP approach

Formally, the OPP approach requires three ingredients: (i) a baseline projection, (ii) impulse response functions (IRFs) for policy shocks, and (iii) a loss function. Based on these three ingredients, one can formulate a linear-quadratic policy problem whose solution delivers an OPP for policy instruments and variables of interest (see Dengler et al. (2024) and de Groot et al. (2021) for technical details and various applications).

The baseline projection, i.e. OPP ingredient (i), provides the reference point for the OPP. It captures how the economy will evolve if monetary policy acts as assumed in the projections. Eurosystem staff projections provide a natural baseline projection for OPPs calculated in preparation of ECB GC meetings. However, the source of the baseline, while important in practice, does not matter for the computation of OPPs from a technical perspective. For example, one could obtain a baseline projection by simulating a structural dynamic stochastic general equilibrium (DSGE) model for a particular macroeconomic shock or by simulating an empirically estimated non-structural model (see e.g. McKay and Wolf, 2023).

The policy IRFs, OPP ingredient (ii), capture how monetary policy can affect macroeconomic variables of interest, such as inflation and real output, by announcing changes in its instruments that materialise today and/or in future periods. The IRFs reflect the response of agents in the economy, such as private households or firms, to an exogenous contemporaneous or announced future shock to a policy instrument. Importantly, since agents are forward-looking, the anticipation of future policy changes affects the response not only in those periods in which the policy change is implemented but already in the periods leading up to the policy change. Figure 1 illustrates this feature by showing IRFs for selected macroeconomic variables to interest rate (news) shocks that are all revealed in the first period but materialise at different time horizons (see upper left panel).1 Capturing the anticipation of future policy adjustments and the behavioural response to them is crucial for the OPP approach to avoid being subject to the Lucas Critique, which states that policy counterfactuals need to take into account that expectations and hence the behaviour of agents are not invariant to policy changes.

Figure 1: Illustration of impulse responses to interest rate news shocks announced in the first period but realised at different time horizons


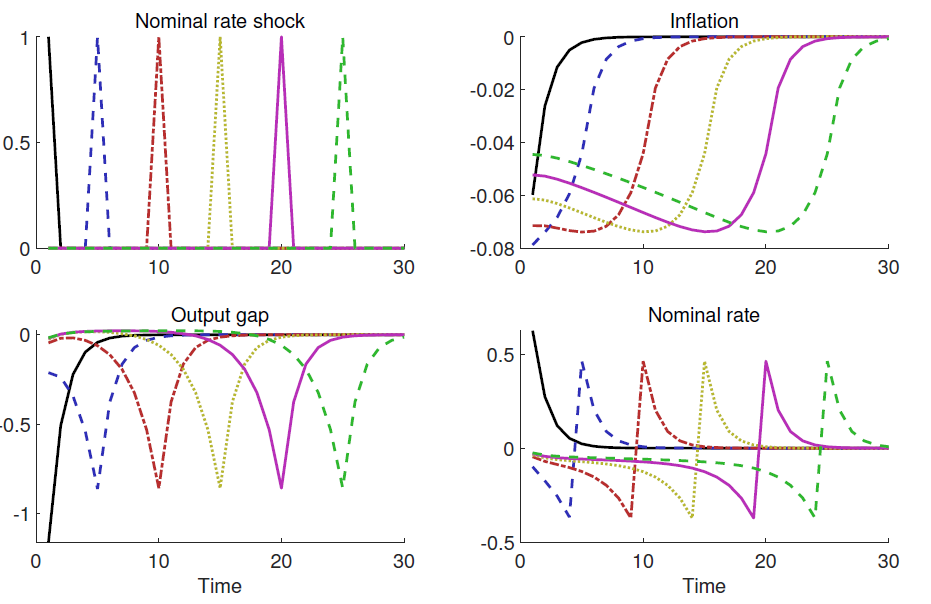
Note: All variables are expressed in percentage deviations from steady state.

Given a baseline projection, the policy IRFs allow to perform policy counterfactuals by implementing an arbitrary interest rate path and assessing its macroeconomic consequences. This is possible due to the key underlying assumption of a linear relationship between macroeconomic variables. Consider the interest rate as a policy instrument. Loosely speaking, the linearity allows constructing arbitrary interest rate paths by adding interest rate (news) shocks to the interest rate path associated with the baseline projection until the desired path is obtained. Importantly, the construction of this interest rate path does not only use the policy shocks but also the IRFs for the interest rate itself to the shocks.2 Due to linearity of the assumed relationships, the IRFs are, weighted with the policy shocks, simply added to the interest rate path associated with the baseline projection. Once the appropriate policy shocks are found to obtain a specific interest rate path, which boils down to a straightforward linear algebra operation, one can calculate the paths for the macroeconomic variables of interest, combining them with the respective baseline projections and IRFs.

The goal of the OPP approach then is to find a very specific counterfactual interest rate path: the path that is optimal according to a loss function (approximately reflecting policymakers’ preferences). The loss function, which is the third and final OPP ingredient, captures these preferences, permitting to rank different time paths for variables of interest. For the GC, the loss function should reflect the mandate of the Eurosystem. This mandate, as specified in the European Treaties, has an explicit primary focus on price stability, but allows monetary policy to pursue certain additional goals if doing so does not interfere with price stability. Formally, the loss function penalises quadratic deviations of variables of interest, like inflation or the output gap, from the respective target values. With respect to inflation for example, many central banks have an explicit numerical target, which would be a natural target value for the loss function. The quadratic penalty expressions are weighted against each other. This is done both within periods, to prioritise the stabilisation of some variables over others, and over time, to reflect the intertemporal dimension of the policy problem. The loss function thus translates a certain path for var-iables of interest into one numerical value.

Together, the three OPP ingredients allow the formulation of a linear-quadratic policy problem that reflects the policymaker’s trade-offs and aims at minimising the loss associated with the feasible time paths for target variables and policy instruments. Ideally, the policymaker would like to choose its instruments to set all penalties to zero, i.e. perfectly stabilise the target variables. In practice, this will often not be feasible. For example, a cost-push shock that is both inflationary and contractionary does not allow the policymaker to stabilise inflation and real economic activity at the same time. What is feasible crucially depends on the baseline projection as a reflection of the status quo, for example output and inflation moving into opposite directions following a cost-push shock, and the IRFs, which reflect the ability of monetary policy to change the status quo, given the structure of the economy and its current state.

The straight blue lines in Figure 2 show the optimal interest rate response under commitment to a persistent cost-push shock (upper left panel) in the canonical New Keynesian model and the associated paths for inflation and the output gap, all expressed as percentage deviations from their long-run values. The loss function used in this case features inflation and the output gap as input arguments.3 While the optimal policy responds to the shock by raising interest rates, it does so only over time and not immediately, reducing the contractionary impact of the shock on real economic activity in the first periods.

Figure 2: OPP for a persistent cost cost-push shock

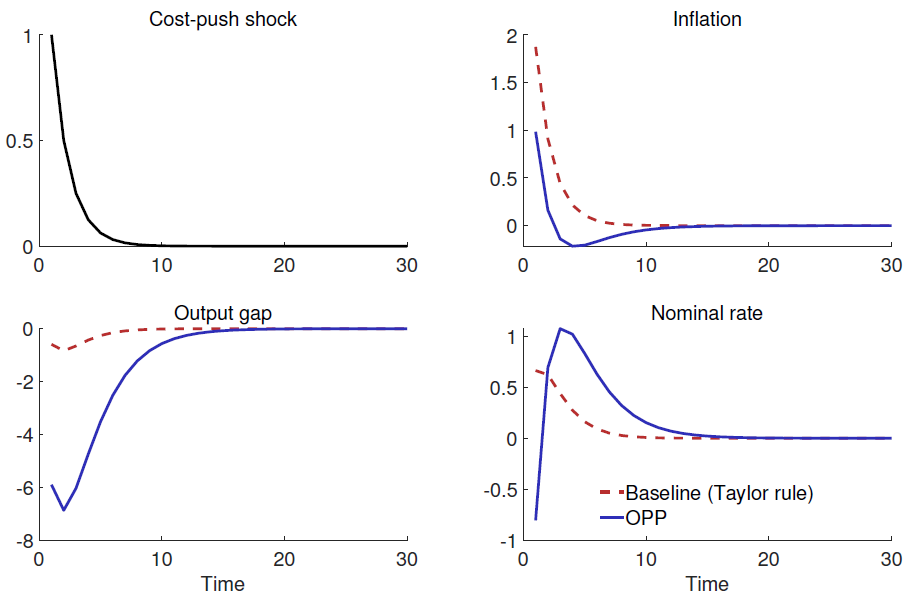
Note: All variables are expressed in percentage deviations from steady state. “Baseline” refers to the model response to the costcost-push shock under an interest rate feedback rule (see Dengler et al., 2024), “OPP” to the optimal policy response.

Two applications

The previous section showed OPPs that took the baseline projection, the policy IRFs and the loss function all from the same simple model. In this section, we show results for two different applications, highlighting the versatility of the OPP approach.

Staff projections for the euro area provide a natural baseline for optimal policy considerations in the context of the Eurosystem. We now use as the OPP baseline the projections of the Broad Macroeconomic Projection Exercise (BMPE) for June 2023, jointly carried out by staff of the ECB and the national central banks of the Eurosystem. To obtain meaningful policy recommendations, it is important to use policy IRFs for the OPPs that capture monetary policy transmission in an empirically plausible way. One way to do this is to take a sufficiently complex DSGE model estimated on relevant macroeconomic data. In the following, we use an extension of the model documented in Gerke et al. (2022). Specifically, the model includes a detailed fiscal policy sector, allowing for rich monetarymonetary-fiscal interactions. For the loss function, we use year year-onon-year inflation deviations from a target value of 2%, output gap deviations from zero to capture real economic activity, and interest rate changes over time to capture (approximately) an aversion towards strong financial market volatility. This specification and the relative weights used in this case are supposed to capture the monetary policy mandate of the Eurosystem (see Deutsche Bundesbank, 2023, for details). For the purpose of illustration, we assume that the nominal interest rate is the only available policy instrument for the exercise. Figure 3 shows the OPP results. Compared to the interest rate path expected by financial markets in June 2023, the OPP OPP-implied path is more restrictive in the first quarters of the projection horizon (left panel), reflecting that inflation was too high from the perspective of the loss function.

Figure 3: OPPs for a medium medium-scale DSGE model based on the June 2023 BMPE


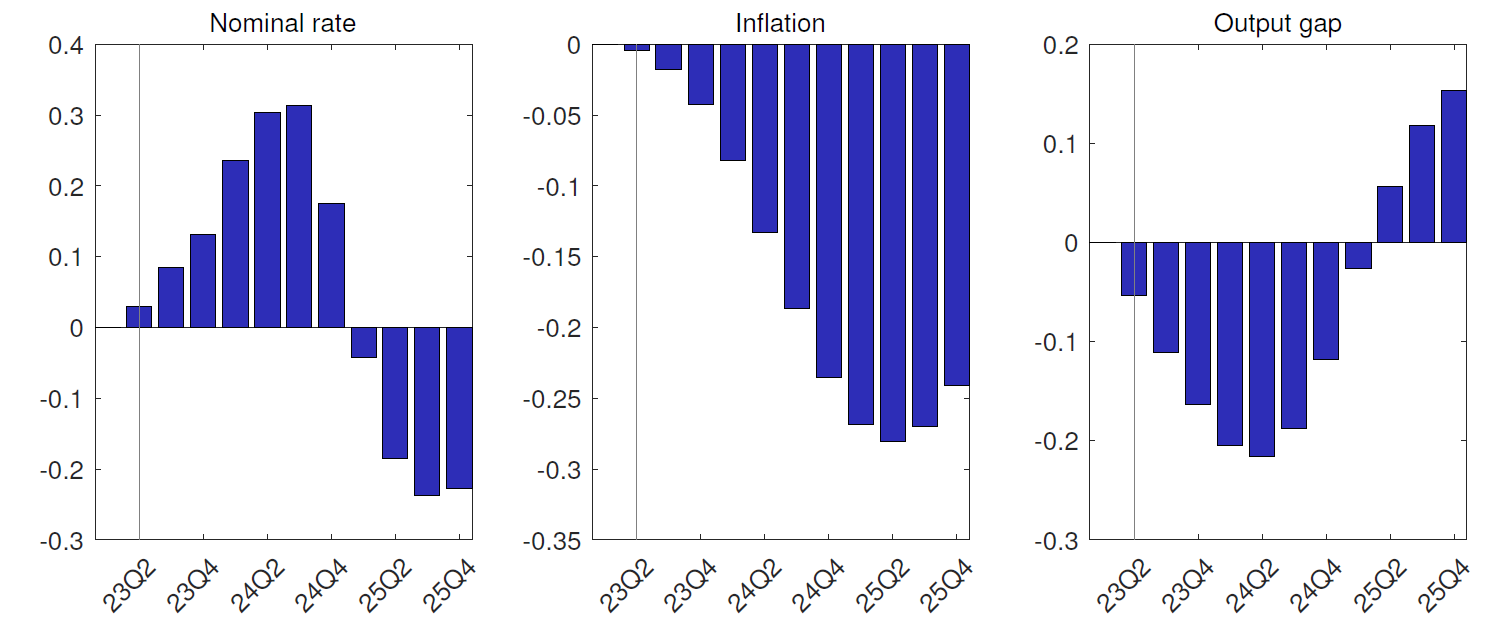
Note: All variables are shown for the OPP and expressed relative to the June 2023 BMPE baseline. The nominal rate is expressed in absolute deviations of the OPP from the baseline (both in annual percentage points). Inflation is expressed in cumulative absolute deviations of the OPP from the baseline (both in annual percentage points). The output gap is expressed in absolute deviations of the OPP from the baseline (both in percent).

An advantage of the OPP approach is that, once one has calculated policy IRFs, one can compute optimal policies for different baseline projections. While the computation of the IRFs itself can be quite challenging, e.g. if the underlying model features substantial heterogeneity on the household or firm side, the OPP approach can also be used for policy simulations in such instances. To illustrate this, Figure 4 shows OPPs for a contractionary cost cost-push shock based on a heterogeneous heterogeneous-agent New Keynesian (HANK) model under different assumptions about the labour supply of households (see Gerke et al., 2024, for details). To isolate the impact of differences between the model versions regarding the transmission of monetary policy, we use the same baseline projection for the three considered model versions, namely the response of the economy in a model version with a representative household (RANK) under an interest rate feedback rule. The RANK model version does not feature heterogeneous households, serving as a benchmark (dotted yellow lines). The HomLS HANK case features households that differ in wealth and income, but abstracts from heterogeneity in hours worked (solid blue lines). The HetLS HANK case relaxes this assumption and allows hours to vary across households, offering insurance device against shocks at the household level (dashed red lines). The assumed specification of the loss function is ad hoc, containing inflation, the output gap and interest rate changes as input variables. Qualitatively, the policy response does not depend on whether households are heterogeneous in income, wealth or hours worked. Quantitatively, however, the responses differ, reflecting that monetary policy transmission is less strong under heterogeneous household labour supply, requiring stronger interest rate hikes to bring down inflation.

Figure 4: OPPs for a cost cost-push shock in model versions with heterogeneous households


Note: All variables are expressed in percentage deviations from steady state. HANK (HomLS): model version with heterogeneous households and homogeneous labour supply. HANK (HetLS): model version with heterogeneous households and heterogeneous labour supply. RANK: model version with representative household.

Concluding remarks

OPPs are a flexible tool to formulate monetary policy trade trade-offs and come up with a quantitative answer to the question: What does the appropriate monetary policy stance look like for a given macroeconomic outlook? However, it is important to emphasise that the OPP approach relies on various potentially restrictive assumptions and does not capture many aspects that are relevant for policymakers in practice (see Dengler et al., 2024, for details). For example, they cannot capture certain nonlinearities like a sovereign default or a financial crisis. Moreover, the OPP inputs, i.e. the baseline projection, the IRFs and the loss function, are all subject to considerable uncertainty. Therefore, while helpful, OPPs should only be used with caution and only as one of many inputs to make well well-informed monetary policy decisions.