Assessing the liquidity premium in the Italian bond market

This paper analyzes the prices of Italian sovereign bonds to study the effects of time-varying liquidity, and proposes a methodology to estimate the liquidity premium implicit in bond prices. After correcting for different maturities and coupon rates, we compute a yield spread between on- and off-the-run ten-year BTPs and regress this quantity on seven well-established liquidity measures, explicitly distinguishing between current and future liquidity. We find that higher liquidity does indeed reflect in higher prices. Moreover, according to our novel estimate of the liquidity premium, the liquidity deterioration occurred during the sovereign debt crisis lasted longer but with smaller magnitude than that registered during the Covid-19 pandemic.

What is liquidity? Why is it important? How can we measure it?

An asset is said to be liquid when it can be traded quickly, with low transaction costs and with minimal impact on the price (Kyle 1985, Engle and Lange 2001, Foucault et al. 2013). Given two identical assets differing in the liquidity profile only, it is intuitive to postulate that the more liquid one shall be valued more. However, it is difficult to empirically isolate the premium agents attach to liquidity, because asset prices summarize not only the degree of liquidity, but also intrinsic characteristics (e.g. coupon rate, maturity, credit risk, etc.), which are rarely the same for different assets. Moreover, traders with different needs monitor and prioritize different aspects of liquidity (e.g. tightness, depth, resilience, etc.). Finally, it is not entirely clear whether prices shall reflect current liquidity or agents’ expectations of future liquidity.

Relying on the theoretical framework pioneered by (Goldreich, Hanke and Nath; 2005), we exploit predictability in the life cycle of 10-year Italian BTPs to assess the impact of liquidity on prices and estimate the liquidity premium. The Italian government finances its national debt issuing bonds on a regular schedule. Newly-issued securities are called “on-the-run” and typically attract the majority of trades, while older bonds are called “off-the-run”. Being more sought-after, “on-the-run” bonds shall be more liquid and, thus, they should have higher prices and lower yields. After correcting for different residual maturity and coupon rates, the “on-the-run” and the first “off-the-run” bonds shall be identical assets in terms of intrinsic characteristics. Therefore, any difference in yields and prices shall be attributed to different expected degrees of liquidity over their remaining life.

We rely on 41 off/on-the-run pairs of 10-year Italian BTP to construct a time-series of yield differential between April 2000 and May 2023. We compute seven different measures of liquidity to ideally capture the multi-faceted nature of liquidity: bid-ask spread, (Roll; 1984), (Corwin and Schultz; 2012), (Abdi and Ranaldo; 2017), (Hui and Heubel; 1984), (Amihud; 2004), and Volume. We assume traders have perfect foresight and approximate the expectation of future liquidity conditions at time t with the average of each measure from time t to T.

Does liquidity affect bond yields?

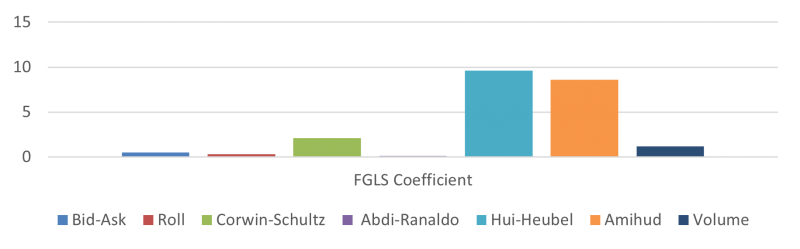
Our first goal is to evaluate the hypothesis that higher future expected liquidity reduces bond yields. For each liquidity measure, we regress the off-on yield differential on the off-on difference in average future measure including fixed effects for each pair of bonds. We find that a positive difference in the average future liquidity measure does indeed increase the yield differential (i.e. off-the-run bonds are less liquid and consequently have higher yields with respect to on-the-run ones).

Figure 1: Baseline Regression

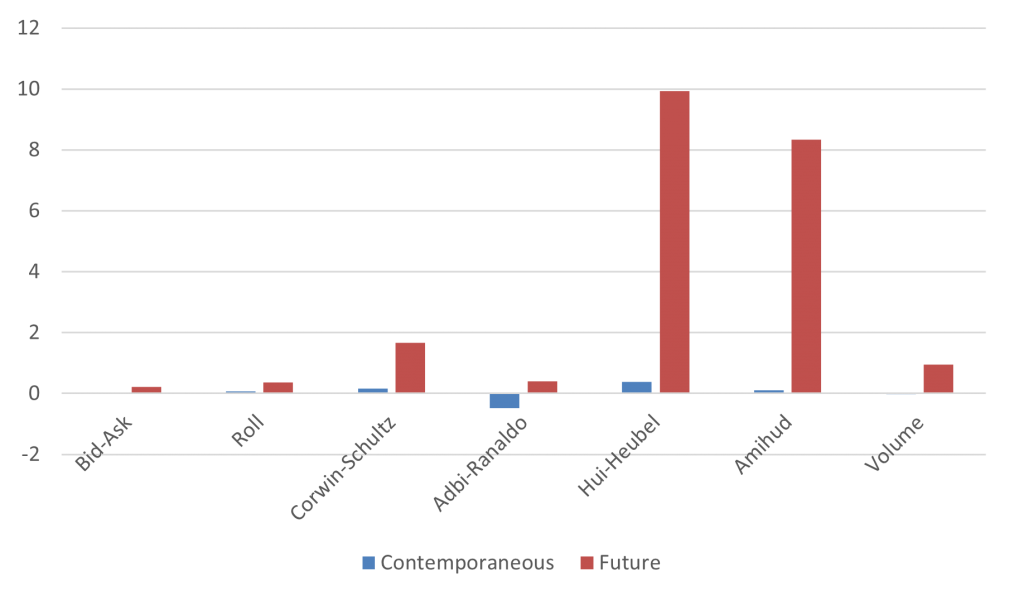
Then, we tried to disentangle the role of current and future expected liquidity. For each measure, we regress the off-on yield differential on the liquidity measure at time t and on the average of the measure from time t+1 to T including fixed-effects for bond pairs. We find that future expected liquidity remains the main driver of yield differentials, above and beyond the impact of current liquidity. Coefficients on future expected liquidity measures are just slightly affected by the inclusion of contemporaneous measures, which in turn display much smaller economic significance.

Figure 2: Contemporaneous and Expected Liquidity

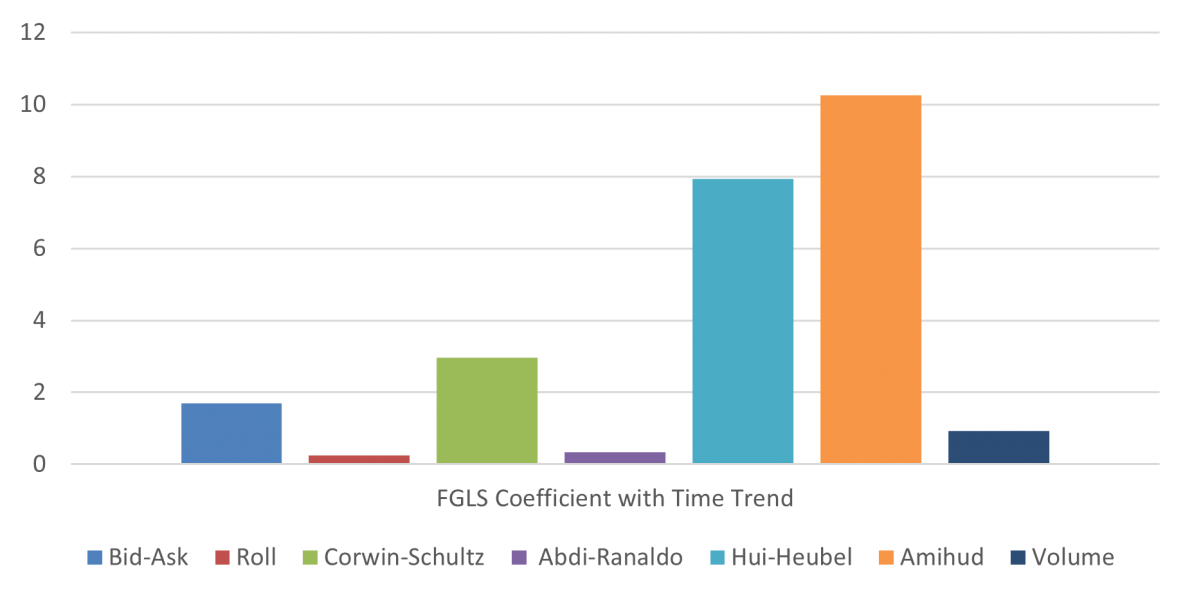
Since bond issuance cycles are predictable, on- and off-the-run bonds become more similar as a new issuance round approaches. To rule out the possibility that our results depend on this mechanical relation, we regress the yield differential on future expected liquidity measures including a time trend and fixed effects. We find that the time trend has a negative coefficient (i.e. yield differential mechanically shrinks with time), but measures of future liquidity still maintain positive coefficients of similar magnitude if compared with the baseline regression.

Figure 3: Time and Expected Liquidity

The premium for (il)liquidity and monetary policy

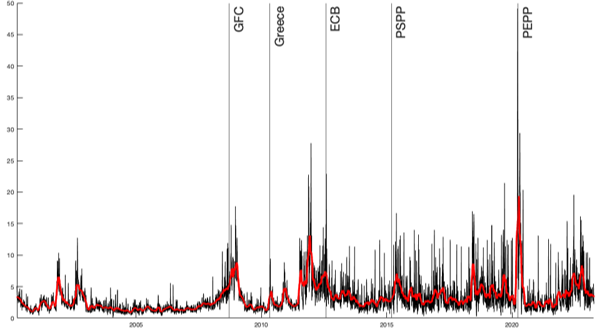
Our theoretical framework implies that yields can be decomposed into a “perfectly-liquid” component (summarizing all intrinsic characteristics assuming perfect liquidity) and a liquidity premium (a penalty for the imperfect liquidity profile). We compute seven different premiums multiplying each liquidity measure by the coefficient obtained from the baseline regression. Then, we average these to obtain a novel aggregate estimate of the liquidity premium on 10-year Italian BTPs. According to our estimates, the liquidity premium for the 10-year BTPs remained stable around historically low values until the Great Financial Crisis, when it increased up to roughly 17bps. During the sovereign debt crisis it surged up to 28 bps and since then its volatility has never returned to pre-crisis levels. During the acute initial phase of the COVID-19 pandemic the premium peaked to its highest record at 50bps.

Figure 4: Liquidity Premium

As a final exercise, we apply the empirical framework developed in (Altavilla et al.; 2019), in order to evaluate the impact of monetary policy on the liquidity premium on Italian government bonds. We find that unanticipated cuts in interest rates compress the premium, that forward guidance suggesting expansive monetary policy reduces the premium as well albeit with halved power, and that quantitative easing has no statistical impact on the premium. (Ferdinandusse et al.; 2020) explain our last finding, showing that the degree of QE effectiveness on liquidity conditions hinges on the share of preferred-habitat investors in the market, and that bonds of peripheral European countries are targeted by a lower share of such investors. It is, however, possible that we do not find an impact of QE, if purchases had largely been anticipated or if the effect slowly propagated over time. In conclusion, the ineffectiveness of QE on liquidity conditions corroborate the conscientious approach the ECB took in designing asset purchases, mitigating unintended scarcity problems in bond markets.