CCPs United: the hidden dangers of shared clearing membership

In centrally cleared markets, a central counterparty (CCP) sits at the centre of transactions, becoming the buyer to every seller and the seller to every buyer. In practice derivatives clearing is characterised by a small set of CCPs. Importantly, a limited number of large banks link these CCPs together, representing the joint clearing membership that together accounts for the lion’s share of clearing volumes. Joint clearing members can play an important role in loss transmission and contagion. Therefore it is important to incorporate these features into current CCP stress-testing practice. Our analysis can serve as a tool to select stress scenarios in markets with multiple central counterparties.

Central clearing is a key feature of global derivatives markets. The mandates to centrally clear derivatives in the aftermath of the Great Financial Crisis (GFC) have considerably altered the shape of financial networks. Centrally cleared markets are characterised by a central counterparty (CCP) which sits at the centre, becoming the buyer to every seller and the seller to every buyer. Theory points to efficiency gains from having a single CCP (Duffie & Zhu, 2011). In practice, however, derivatives clearing is characterised by a small set of CCPs, rather than a single CCP. Importantly, linking these CCPs is a limited number of large banks that clears across CCPs. This group of banks represents the so-called joint clearing membership, which accounts for the lion’s share of clearing volumes. An example of this can be seen in Figure 1.

Figure 1: Network of clearing members and CCPs

Joint clearing membership has a bearing on the structure of interconnections in financial networks. Indeed, connections between CCPs arise due to the shared clearing membership, and connections between clearing members arise via CCPs. Accordingly, risk transmission in financial networks can be affected (Faruqui et al. (2018)). In the context of centrally cleared markets, a central role in risk transmission is played by the default management mechanism of CCPs. This is usually described in terms of the so-called “default waterfall”, which specifies the order of loss absorption of resources available to CCPs (Duffie (2014)).

Joint clearing membership may affect various layers of the default waterfall. At a general level, the default waterfall can be split into losses paid by defaulters and by survivors. Initial losses are paid for by defaulting members in the form of initial margins and their default fund contributions. Higher losses are paid for by the CCP (through so-called “skin-in-the-game”, i.e. equity) and surviving clearing members (through their default fund contributions and potentially additional contributions). We show that joint clearing membership affects both parts of the default waterfall – namely how both defaulters and survivors pay – and that that this gives rise to different contagion channels.

Two contagion channels are considered. The first is the fire-sale channel of initial margins. Initial margins, typically in the form of collateral, serve as the first line of defence to cover losses. A simultaneous default by a joint clearing member at more than one CCP can lead to losses larger than those covered by initial margins at all the CCPs where the member clears. This situation can be considerably worsened if the collateral used is illiquid, as forced liquidation will have an outsize impact on prices, potentially leading to more losses and defaults.

The second channel we consider is associated with one of the last layers of the default waterfall: variation margin gains haircutting (VMGH). When a stressed CCP uses VMGH it only pays out a fraction of the variation margin it owes while still receiving full payments on the variation margin owed by its clearing members. We show that one CCP’s VMGH can transmit losses to another CCP via their joint clearing members.

These two channels can feed each other. In particular, illiquid collateral and VMGH can interact in way such that illiquid collateral begets higher VMGH which in turn exacerbate losses and generate further pressure to sell illiquid collateral into a thin market. This has the potential to significantly increase losses. Risks arising from this interaction are more prevalent when the CCP-bank nexus consists of cycles, that is, when CCPs are connected to each other via joint clearing members.

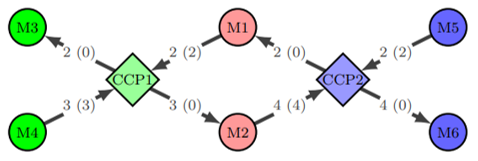
These channels can be illustrated through a network model where clearing members are connected to multiple CCPs through derivatives market obligations.1 The trigger for contagion is an exogenous change in market conditions that sparks variation margins calls between clearing members and CCPs. Counterparties that are not able to fully meet their variation margin calls are put on ”technical default”, and their initial margins and default fund contributions will be used to meet obligations. If the collateral used for initial margins is illiquid, however, the value realised when selling it will fall short of what the face value suggested. This can fuel further shock transmission. If payment obligations cannot be met by these means, clearing members effectively default. CCPs, on the other hand, can rely on VMHG. Effectively this curtails payments to surviving clearing members, contributing to further contagion. Stress can be transmitted at each stage of this process across CCPs and clearing members due to the shared clearing membership. Figure 2 presents a stylised version of the types of network structures we have in mind in the model.

Figure 2: Stylised example of loss transmission to joint clearing members

Case studies calibrated to real data suggest these contagion channels can be relevant in practice. In particular, we use data from the credit default swap and interest rate swap markets to show how contagion increases when all the channels outlined above are simultaneously present (see Veraart & Aldasoro (2022) for a detailed analysis).

There are important implications from a policy perspective, especially regarding CCP stress-testing. Current CCP stress-testing is based on the so-called Cover 2 standard. Generally speaking, this approach seeks to identify the two groups of clearing members that would lead to the largest shortfall of prefunded resources for a given CCP (or alternatively across all CCPs). Our illustrative simulations suggest that the total loss can increase roughly by a factor of four when considering network effects with multiple CCPs, shared clearing members and the contagion channels discussed above. Importantly, our exercise show that who the top two clearing members are (that cause the highest losses) will significantly depend on the contagion channels considered. Concretely, the ranking of institutions according to first order losses can differ notably from that obtained when considering higher order losses that account for shared clearing membership. From a financial stability perspective, it is therefore paramount to consider the network of joint clearing membership across multiple CCPs.

The analysis suggests that stress-testing practice that excludes network effects arising form joint clearing membership risks not being conservative enough. One of the important lessons from the GFC was that stress scenarios need to be “sufficiently severe” (Basel Committee on Banking Supervision, 2018, Principle 4). Our work provides evidence that accounting for network effects and joint clearing membership can be crucial to achieve this objective.