House prices and ultra-low interest rates: Exploring the non-linear nexus

We empirically explore the relationship between house prices and interest rates. Asset-pricing theory suggests that real house prices respond to changes in real interest rates in a non-linear fashion. This non-linearity should be especially pronounced at very low real interest rates. Most existing empirical studies estimate models with a constant semi-elasticity, thereby ruling out by design the potential non-linearities between house prices and interest rates. To address this issue, we estimate a panel model for the euro area countries with a constant interest rate elasticity (as opposed to a constant semi-elasticity), which is consistent with asset pricing theory. Our empirical results suggest that, in a low interest rate environment such as the period between 2015 and 2021, non-linearities in the house price response to interest rate changes are important: an increase of real interest rates from ultra-low levels could lead to downward pressure on real house prices three to eight times higher than the literature suggests.

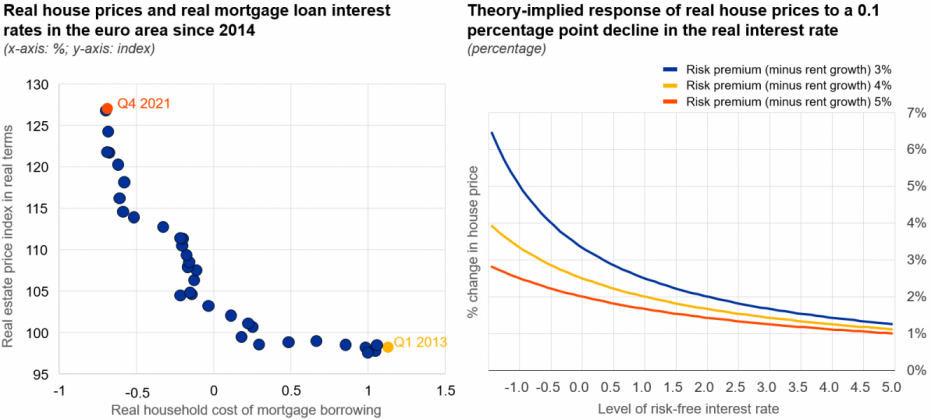
The acceleration of house price growth amidst falling interest rates to record-low levels across euro area countries between 2015 and 2021 has sparked renewed interest in the link between the two variables. Annual euro area residential real estate (RRE) price growth reached 9.5% in Q4 2021—the highest growth rate observed then for over 20 years—while in half of the euro area countries RRE price growth surpassed 10%. At the same time, interest rates on mortgage loans reached a historic low during 2021 of 1.3% in nominal terms. The extent to which changes in interest rates are associated with changes in house prices is foremost an empirical question and measured by the interest rate elasticity of house prices. However, empirical estimates of the interest rate elasticity of house prices vary significantly in the literature (Iossifov, Čihák and Shanghavi, 2008; Adelino, Schoar and Severino, 2012). Importantly, most studies presented above speak of elasticities, while, in fact, they are estimating semi-elasticities (common in log-linear model settings), i.e. percentage changes in house prices in relation to percentage point changes in interest rates. On average, a value for the semi-elasticity of around -3 is reported. This number implies that real house prices should drop by 3% if real interest rates rise by 1 percentage point. At the juncture of rising inflation and monetary policy reversal, elasticity estimates taking into account the specificities of a preceding ultra-low real interest rate environment are crucial for gauging the potential for house price corrections.

Economic theory suggests that real house prices respond to changes in real interest rates in a non-linear fashion. This non-linearity should be especially pronounced at very low real interest rates. Based on a standard asset pricing model without uncertainty, where the price of an asset is equal to the present discounted value of future income streams, one can show that real house prices P_t can be explained by current real rents R_t, expected future real rent growth g^e_t, the expected long-term real interest rate i^e_t, and a risk premium π: log(P_t) = log(R_t) – log(i^e_t + π – g^e_t). This equation implies a unit elasticity of real house prices with respect to real rents and the interest rate term (positive for the former, negative for the latter). This constant unit elasticity results in a non-linear relationship in the response of real house prices to changes in the real interest rate: the lower the level of the real interest rate, the larger should be the response of house prices for a given interest rate change (Figure 1, right). Moreover, lower risk-premia and higher expected rent growth amplify this nonlinearity.

Empirical results for the euro area suggest that in the low interest rate environment of 2015-2021, non-linearities in the house price response to interest rate changes do exist. To confirm the presence of such non-linearities, we estimate two competing model specifications for the log of real house prices across the panel of euro area countries starting in 2010: One with the real interest rate level (constant semi-elasticity) and one with the log real interest rate term (constant elasticity) as an explanatory variable.  Only the log-log specification results in a coefficient that can be interpreted as a true elasticity, and thus captures non-linearities between house price growth and changes in the real interest rate. The results show that the non-linear model specification outperforms the linear one in terms of goodness-of-fit by 1.2 to 3.5 percentage points, depending on the start of the estimation sample (Figure 2, left). In addition, the elasticity estimate converges towards the theory-implied value of unity for estimation samples that mainly cover the low interest rate environment of the past few years. Both results point to the existence of meaningful non-linear effects in the response of real house prices to changes in the real interest rate.

Indications of this non-linearity can also be found when repeating the same exercise as above at the country level. In Figure 2 on the right-hand side, we plot country-specific elasticity estimates (of the log-log specification starting in Q1 2014) against the difference in goodness-of-fit between the non-linear and linear model specification. We find that in most euro area countries (except for in Italy, Cyprus, Finland, Malta, and Greece) the non-linear model fits the data better in recent years, with the difference in goodness of fit of up to 6% for the sample starting in 2014. Furthermore, the estimated elasticity is not too far away from the theory-implied unit value, with most country specific estimates of the elasticity lying between 0.5 and 1.5.

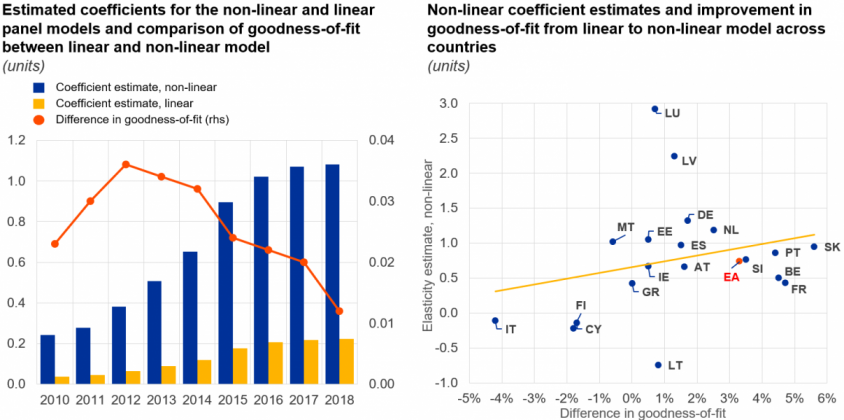
Notes: A positive difference in goodness-of-fit indicates that the non-linear model outperforms the linear model and vice versa.

 

The negative non-linear relationship between real house price growth and changes in real interest rates has important implications in a low real interest rate environment. First, a bigger fraction of observed real house price growth between 2015 and 2021 may be due to declines in real borrowing costs for households. Second, the potential downward pressure on real house prices from rising real interest rates from such a low level as observed between 2015 and 2021 might be substantially larger than what conventional econometric models would suggest. We use our panel elasticity estimates and Q4 2021 aggregate euro area data to predict the marginal house price response to a hypothetical 0.1 percentage point increase (over one quarter) in the real household cost of borrowing for house purchases. Figure 3 displays the results for the estimated models using data starting in 2013 and in 2016.

There are several take-aways from Figure 3. First, the estimated house price response depends strongly on the sample starting date. Starting the estimation sample in 2016 when rates began to venture into ultra-low territory, roughly doubles the expected marginal response from the non-linear log-log model specification compared to a model estimated on a sample starting in 2013. This is reflective of the heightened sensitivity of house prices with respect to changes in interest rates estimated when interest rates are very low.  It is important to note, however, that the estimated house price response is marginal with respect to the simulated 10 basis point increase in the real cost of borrowing. Every successive 10 basis point increase will have a slightly lower impact overall, due to the non-linear nature of the relationship.

Second, Figure 3 shows that the size of the estimated house price response depends crucially on the level of the real interest rate at which its change occurs. In line with the non-linear relationship, the response is accentuated when interest rates rise from a lower level like in 2017 or 2021, as shown above. Third and last, the figure shows the response difference between a linear and non-linear model for the different estimation samples and initial interest rate levels. Obviously, the linear response is independent of the interest rate level. As of Q4 2021, where the euro area average real household cost of borrowing stood at -0.69%, this would result in a difference of around 25 basis points for both estimation start dates between our non-linear specification and a conventional linear one.

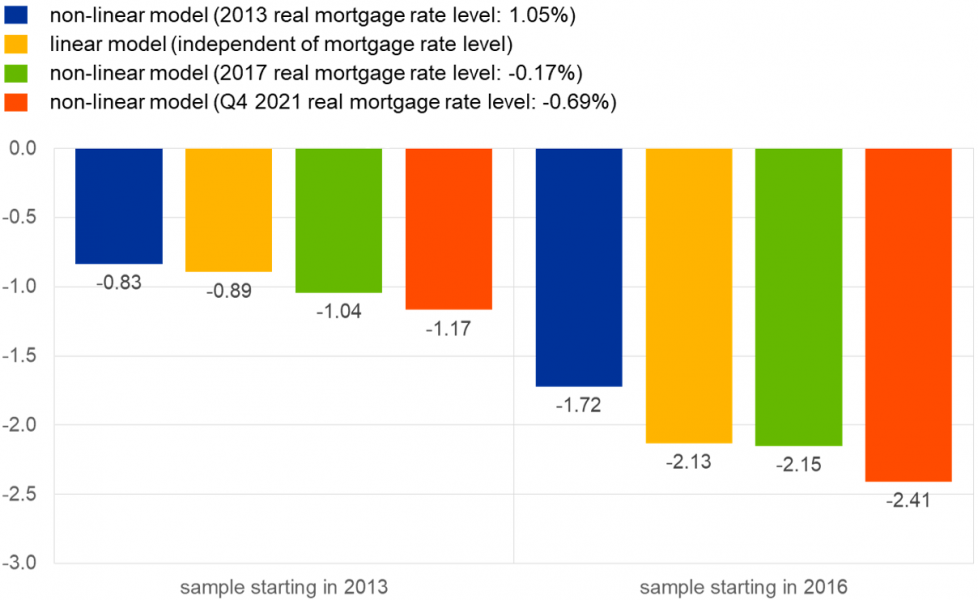
In summary, based on the panel elasticity estimates above and the Q4 2021-level of real interest rates, an increase in real interest rates by just 0.1 percentage points within one quarter could lead to downward pressure on real house prices of between -2.4% and -1.2% across euro area countries, depending on which estimation start date is chosen to obtain the elasticity estimates. Compared to the literature’s average semi-elasticity estimate of -3, which implies a -0.3% change in house prices for a 0.1pp increase in the real interest rate, we retrieve a house prices response that is four to eight-fold as strong in an environment of very low real interest rates. When compared to the linear model on the same estimation sample, the difference (i.e., between the red and yellow bars in Figure 3 above) in the impact on real house prices of a 0.1pp change in the real interest rate comes out to 28 basis points at the end of the sample.

We find in our analysis that, in a low interest rate environment such as the period between 2015 and 2021, non-linearities in the house price response to interest rate changes are important as evidenced by better performance of the model that allows to capture non-linearities (a model with a constant elasticity) compared to the model which allows to capture linearity only (a model with constant semi-elasticity). Taking the ultra-low interest rate level of Q4 2021 as an example, an increase of real interest rates by 0.1 percentage points could lead to downward pressure on real house prices in the range of -2.4% and -1.2% which is about four to eight-fold the magnitude the literature would predict. Our findings are highly relevant for policy makers as sharp declines in house prices, especially after long periods of credit-sustained expansion, have historically been frequently associated with banking crises (Jordà, Schularick & Taylor, 2015; Baron & Dieckelmann, 2022). A sharp increase in the real household cost of borrowing or, more generally, of real interest rates, could affect banks’ financial health either through increases in difficulties of households to repay their loans and a resulting rise in non-performing loans or through a medium-term bank-profitability channel, depending on the country’s mortgage rate regime. At the juncture of rising inflation and monetary policy reversal, elasticity estimates taking into account the specificities of a preceding ultra-low real interest rate environment are crucial for gauging the potential for house price corrections.