

This paper estimates the volatility index term structure for the Spanish bank sector (SBVX) from 2015 to 2021 using the implied volatility of individual banks and assuming that correlation risk premium in the banking sector is proportional to the market’s (Ibex-35). One-year SBVX informs about the dynamics of bank returns beyond the standard market volatility index VIBEX, especially when bank returns are negative. If positive, bank returns relate to the dynamics of VIBEX just as much as SBVX, which aligns with the belief that a drop in global volatility (uncertainty) positively affects firm performance and, therefore, bank value projections. We also find one-month SBVX outperforming VIBEX to forecast monthly bank returns volatility. Our results suggest using SBVX term structure, short-term VIBEX, and market correlation risk premium to monitor uncertainty and returns in the banking sector and foresee periods of stress. This paper contributes to research that estimates the banking sector’s sensitivity to uncertainty, volatility, and risk.
Although estimating global volatility is crucial to identify and anticipate the impact of uncertainty shocks on the real economy and financial markets, we also need to assess an accurate and informative estimation of idiosyncratic volatility. It is essential to foster the study of uncertainty heterogeneity and spillovers across portfolios to generate a theory around its dynamics and interactions with economic variables. This paper contributes to the growing literature that assesses market-based portfolio volatility measures and provides a volatility index for a portfolio that tracks the Spanish banking sector. We show that the SBVX term structure exhibits additional information not provided by the market that can be used to monitor the dynamics of current and future banking sector returns.
But how does uncertainty impact the banking sector returns? Previous studies find that uncertainty (primarily economic policy uncertainty) affects the banking industry through different channels. In particular, uncertainty affects aggregate bank lending (Danisman et al. (2021), Talavera et al. (2012), among others), with heterogeneous effects across banks (see Buch et al. (2015)), which results in evidence of a negative relationship between uncertainty and bank valuation (see He & Niu (2018) and Danisman et al. (2021)). More recently, Kerry (2020) and Haldane (2012), among others, advise using equity markets, besides accounting ratios, to estimate market-based uncertainty measures to identify turmoil in the banking sector. Our article aligns with this literature and calculates a market-based uncertainty measure for the banking sector. However, unlike previous literature, we suggest using option prices to reach this goal besides the equity market prices.
International investors frequently use the VIX to approach global volatility and risk perception. Since the VIX relies on the price of S&P500 options, the S&P500 is considered a good proxy for the worldwide market. However, if portfolio options exist, creating volatility indices for other market definitions is possible, even for other asset portfolios. It is not our case. We define a portfolio (with no liquid options) to approach the banking sector and estimate the portfolio volatility index term structure, labeled SBVX. We reach our goal working in the framework described in Buss and Vilkov (2012). However, we assume that the correlation risk premium for the banking sector and the market are proportional as a novelty. This assumption implies that the uncertainty compensation associated with the future banking portfolio correlation is proportional to the compensation discounted for the market portfolio; this is a belief that the market does not contradict. In our case, we identify the market (reference) portfolio with the Ibex-35 and the non-traded portfolio with the Spanish banking sector, so we assume that uncertainty compensation in the Ibex-35 and Ibex-35 bank portfolio are proportional. The researcher may choose alternative reference (market) portfolios as far as the risk-neutral volatility of such a portfolio exists (e.g., S&P 500, S&P 100, Euro Stoxx 50, Euro Stoxx Banks, etc.).
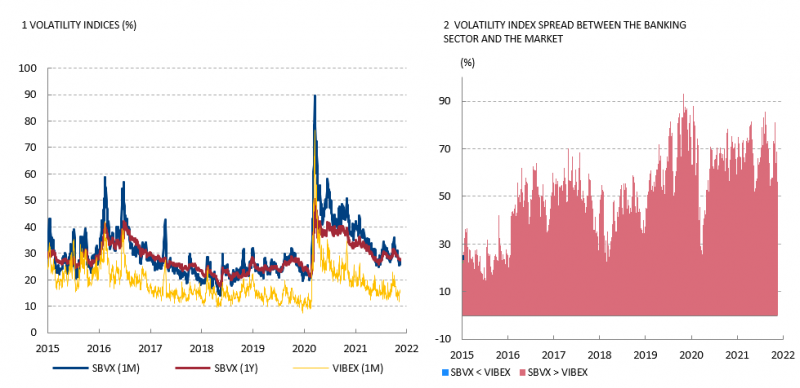
The constituents of our banking sector portfolio are the BBVA, Santander, Bankia, Caixabank, Sabadell and Bankinter. Portfolio weights normalize to Ibex-35 banks’ stock index composition, including the abovementioned banks. We also calculate the VIBEX term structure from Ibex-35 options. The market only estimates one-month VIBEX, and the correlation risk premium tenor must pair with the SBVX tenor. Figure 1 includes the resulting daily SBVX series for one-month and one-year tenors from 2015 to 2021 and the one-month VIBEX. Several conclusions arise from the figure. In contrast to market volatility indices, the SBVX term-structure slope tends to be negative (backwardation) more frequently than the market volatility index. This evidence suggests that banking sector uncertainty tends to concentrate in short tenors in stress times, a behavior we also confirm for other European volatility indices associated with the banking sector, such as the ATM implied volatility for the SX7E stock index. The banks-market volatility gap increased in 2016, fostered by further integration of the banking and financial sector that made the banking portfolio less diversified. We observed a gap reduction at low volatility times (2018) and in turmoil periods, as in March 2020, when the Covid-19 event impacted the banking sector’s uncertainty as much as other sectors. Additional research in Gonzalez-Perez (2021) finds the volatility gap and the realized volatility in the banking sector positively related. According to this result, when bank volatility increases in the stock market, we usually see a rise in the market-bank volatility index gap, suggesting that sector-distinctive factors drive the upward movement in volatility. Finally, the SBVX series is on average higher than VIBEX but also less volatile than VIBEX, in line with the market belief that uncertainty is more stable for banks than for the market. On average, a 1% increase (decrease) in one-month SBVX associates to a raise (decline) of +3.9% (-3.9%) of one-month VIBEX.
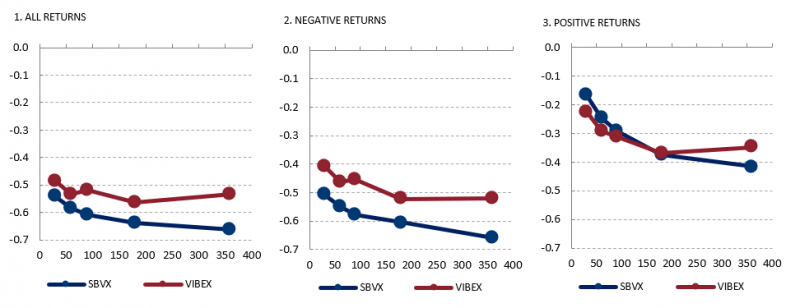
The literature refers to the leverage effect as the negative relationship between asset returns and changes in its volatility. Thus, as asset prices decline, firms become more leveraged since the relative value of their debt rises relative to that of their equity, see Black (1976) and Christie (1982), so that the asset becomes riskier, hence more volatile. This empirical evidence is found in all volatility indices and posted in white papers to confirm its utility to measure investor fear gauge and monitor underlying returns. We also find it in the SBVX and VIBEX (see Figure 2, first panel). However, significant differences emerge for each volatility index when we differ between positive and negative banking portfolio returns. While a drop in bank prices relates to higher idiosyncratic uncertainty, an increase in bank prices tends to correlate with lower market uncertainty perception, see Figure 2 (second and third panels). This result confirms the idiosyncratic predominant uncertainty component when bank shares drop and aligns with literature that finds a robust negative relationship between market uncertainty and bank value due to a reduction in non-performing loans. Overall, our findings recommend using banking-specific volatility indices in addition to market proxies to study the impact of uncertainty in the banking industry return dynamics under different scenarios.
Figure 1. Volatility indices and bank-market volatility gap (log-ratio).
Some authors claim that the leverage effect may be driven exclusively by outliers, so returns in the continuous part of the distribution do not relate as strongly as in the tails. However, the distribution of jumps in SBVX confirms a significantly low proportion of observations above two standard deviations, especially for one-year SBVX (0.9%). This tenor reports a higher correlation coefficient. So we conclude that this claim does not play a role in our exercise.
Figure 2. Linear correlation coefficients for different tenors (horizontal axis, number of days) between returns in Ibex-35 bank and each volatility index (SBVX and VIBEX). Sample: 2015-2021.
After testing the relationship between SBVX and the banking sector returns, we can use it as a natural benchmark to normalize the uncertainty quoted by each banking portfolio constituent. Thus, ups and downs in the relative bank-sector volatility gap for different portfolio constituents can be broadly interpreted as idiosyncratic bank volatility. The ratio dynamics would relate to various economic or financial events affecting each institution’s market value expectations. We can also generate measures of the level of sector integration by looking at the joint bank-sector volatility gap distribution. Our results recommend using SBVX to normalize individual implied volatility series to foresee excess uncertainty or volatility times for individual banks and monitoring bank returns dynamics.
To determine the volatility indices’ forward-looking component, we explore the ability of VIBEX and SBVX to forecast banks’ returns volatility. We find short-term SBVX better one-month banking returns volatility predictor than the market. Further statistical details in the paper Gonzalez-Perez (2021). Therefore, while long maturity SBVX and VIBEX form part of the same uncertainty palette to understand current returns dynamics in the banking sector, short-term SBVX seems preferable to forecast the volatility of bank returns. The change in the preferable tenor would result naturally since short-term volatility indices are more sensitive to the arrival of new information that may affect future bank returns and volatility. Hence, obtained results confirm the significant role of the SBVX term structure in monitoring bank share returns and volatility in the equity market beyond the VIBEX.
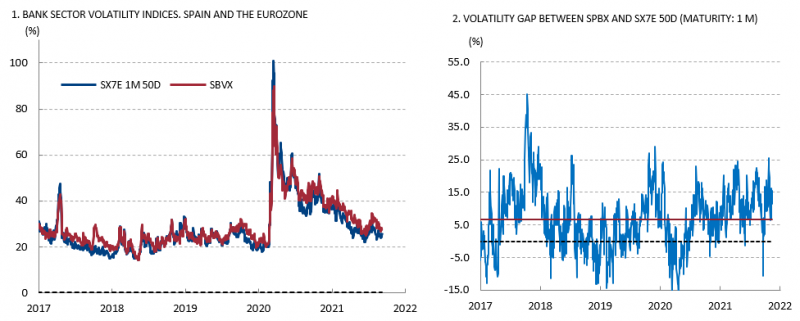
As the last exercise to illustrate the SBVX information content and utility, we compare SBVX with the volatility index for Eurozone banks; the ATM implied volatility for the EURO STOXX Bank index (SX7E) provided by Bloomberg. Eurozone data started in 2017, Figure 3 relates the series since then. Both volatility indices exhibit a similar pattern. However, SBVX wanders around the SX7E volatility index, revealing a positive gap around 6.5% higher than the SX7E volatility index over the whole sample. The Eurozone banking index is more diversified than the Spanish, covering different countries, which helps to explain the average gap. However, the short-term gap dynamics may contain helpful information to address the relative uncertainty by region. One market turmoil episode of interest occurs around the Covid-19 shock. In this period, the volatility gap inverted, and the Spanish banking sector quoted significantly less uncertainty than the Eurozone as a whole. Being aware of differences in investors’ uncertainty price for the banking sector around financial or economic policy turmoil is relevant to enhancing financial stability and macroprudential exercises. SBVX index makes this exercise easier. Future analysis, currently in progress, will bring more light to this topic.
Figure 3. ATM implied volatility indices for the Spanish bank portfolio (SBVX) and the Eurostoxx 50 banks (SX7E) for one-month maturity.
After the developed analysis, we found many potential uses of the SBVX term structure. Although the list of possible SBVX uses is more extensive, let’s summarize those described in this document. (1) Monitoring individual banks and the banking sector returns, forecasting realized volatility and studying the asymmetric impact of uncertainty on banking returns. (2) Normalize uncertainty for each bank and foresee periods of turmoil or stress per each of them. (3) Differentiate between the banking sector uncertainty priced domestically and in the Eurozone.
Finally, it is possible to estimate the SBVX using different weights (following further banking sector characterization) or other reference portfolios. Ours is a baseline approach that uses the Ibex-35 as a reference portfolio and fair assumptions about the banking sector’s correlation risk premium. The methodological contribution and results supplied contribute to financial stability and macroprudential exercises keen to monitor banking sector uncertainty drivers and dynamics. Further technical details of this study are available in the paper, Gonzalez-Perez (2021).
Black, F., (1976) ‘Studies in stock price volatility changes.’ In: ‘Proceedings of the 1976 Meeting of the Business and Economic Statistics Section’. American Statistical Association, pp. 177–181.
Buch, C., Buchholz, M. & Tonzer, L. (2015), ‘Uncertainty, bank lending, and bank-level heterogeneity’, IMF Economic Review 63, 919–954.
Buss, A. & Vilkov, G. (2012), ‘Measuring equity risk with option-implied correlations’, The Review of Financial Studies 25(10), 3113–3140.
Christie, A. (1982) ‘The stochastic behavior of common stock variances -Value, leverage, and interest rate effects’, Journal of Financial Economic Theory, 10 (1982), pp. 407-432.
Danisman, G., Demir, E. & Ozili, P. (2021), ‘Loan loss provisioning of us banks: Economic policy uncertainty and discretionary behavior,’ International Review of Economics & Finance 71, 923–935.
Gonzalez-Perez, M.T. (2021), ‘Lessons from estimating the average option-implied volatility term structure or the Spanish banking sector,’ Banco de España Working Paper No. 2128.
Haldane, A. (2012), ‘The dog and the frisbee,’ Bank of England Speech at the Federal Reserve Bank of Kansas City’s 36th Economic Policy Symposium. August.
He, Z. & Niu, J. (2018), ‘The effect of economic policy uncertainty on bank valuations’, Applied Economics Letters 25 (5), 345–347.
Kerry, W. (2020), ‘Using the market value of equity to signal banking sector vulnerabilities’, Journal of Risk management in Financial Institutions 13 (2), 135–144.
Talavera, O., Tsapin, A. & Zholud, O. (2012), ‘Macroeconomic uncertainty and bank lending: the case of ukraine’, Economic system 36 (2), 279–293.
The opinions in this Policy Brief are solely the author’s and do not necessarily represent those of Banco de España or the Eurosystem.