Measuring Regulatory Complexity

Despite a heated debate on the perceived increasing complexity of financial regulation, there is no available measure of regulatory complexity other than the mere length of regulatory documents. To fill this gap, we propose to apply simple measures from the computer science literature by treating regulation like an algorithm – a fixed set of rules that determine how an input (e.g., a bank balance sheet) leads to an output (a regulatory decision). We apply our measures to an algorithm computing capital requirements based on Basel I, and to actual regulatory texts like the Dodd-Frank Act. Our measures capture dimensions of complexity beyond the mere length of a regulation. In particular, shorter regulations are not necessarily less complex, as they can also use more “high-level” language and concepts. Finally, we propose an experimental protocol to validate measures of regulatory complexity.

The great financial crisis of 2007-2008 led to a major overhaul of global financial regulation, as exemplified by the Basel III Accords, the Dodd-Frank Act in the United States, the Bank Recovery and Resolution Directive in the European Union, or the Single Supervisory Mechanism in the euro area. The financial industry quickly complained about the complexity of these new regulations, and the additional burden they would put on the industry. Perhaps more surprisingly, some regulators and regulatory authorities have signaled that they too were concerned about the level of complexity reached by banking regulation. The Bank of England’s Chief Economist Andy Haldane, for instance, voiced fears that bank capital regulation has become so complex that it could be counterproductive and lead to regulatory arbitrage (Haldane and Madouros, 2012). In the United States, the idea that regulatory complexity could impose an undue burden on small banks has led to several proposals to exempt them from a number of rules, provided that they appear sufficiently capitalized (Calomiris, 2018).

Reflecting this shift in the perception of recent regulatory trends, the Basel Committee on Banking Supervision released a discussion paper that conceptualizes regulatory “simplicity”, and postulates the existence of a trade-off between the risk-sensitivity of regulation, its simplicity, and comparability (BCBS, 2013).

In order to operationalize this trade-off and weigh the costs of new regulations in terms of complexity against the gains in terms of precision, regulators need to be able to measure the complexity of potential new regulations. Complexity is of course a very difficult object to measure. For instance, in their seminal “The Dog and the Frisbee” article, Haldane and Madouros use the number of pages of the different Basel Accords (from 30 pages for Basel I in 1988 to more than 600 pages for Basel III in 2014) as a measure of regulatory complexity. While informative, such a measure is quite crude and difficult to interpret. For instance, should one control for the fact that Basel III deals with a significantly higher number of issues than Basel I? Is a longer but more self-contained regulation more or less complex? To guide us through such questions, we lack a framework to think about what complexity means in this context and how it can be measured.

To fill this gap, we propose in a new research paper1 to apply simple measures from the computer science literature by treating regulations like algorithms—fixed sets of rules that determine how an input (e.g., a bank balance sheet) leads to an output (a regulatory decision). Our measures capture dimensions of complexity beyond the mere length of a regulation. We apply our measures to actual regulatory texts, Basel I and the Dodd-Frank Act, and propose an experimental framework to backtest our measures. In doing so, we created a large “dictionary” of regulatory terms, which can be used by researchers and regulators to compute the complexity measures of other texts.

Regulation as an Algorithm

The seminal idea of our paper is to interpret regulation as an algorithm, that is, a series of instructions applied to an input (e.g., a bank balance sheet) that lead to an output (e.g., a regulatory decision). This parallel is perhaps best seen in the computation of capital requirements under Basel I, the regulatory text consisting essentially in a detailed list of the rules to apply in order to compute a bank’s capital requirements. Because of the close parallel between the Basel I rules and an algorithm, we can directly “translate” the text of Basel I into a functioning computer algorithm.

If one accepts this parallel between regulations and algorithms, it becomes possible to use the extent literature on algorithmic complexity to analyze the complexity of regulation. We propose a framework that formally defines different dimensions of complexity that can be captured by a measure of complexity. In particular, we make a distinction between: (i) “problem complexity”, a regulation that is complex because it aims at imposing many different rules on the regulated entities; (ii) “psychological complexity”, a regulation that is complex because it is difficult for a human reader to understand; and (iii) “computational complexity”, a regulation that is complex because it is long and costly to implement. Our measures rely on the analysis of the text describing a regulation, and so our analysis focuses on problem complexity and psychological complexity.

Among the many measures of algorithmic complexity that have been studied in the computer science literature, we focus on the measures pioneered by Maurice Halstead in the 1970s (Halstead, 1977). These measures rely on a count of the number of “operators” (e.g., +,- , logical connectors) and “operands” (e.g. variables, parameters) in an algorithm, and the measures of complexity aim at capturing the number of operations and the number of operands used in those operations. In the context of regulation these measures can help capture the number of different rules (“operations”) in a regulation, whether these rules are repetitive or different, whether they apply to different economic entities or to the same ones, and so on.

Measuring the complexity of an algorithm—and consequently the complexity of a regulatory text—boils down to counting the number of operators and operands. If we wanted to use the length (or “volume”) of an algorithm as a measure of complexity, we could simply use the total number of operators plus the total number of operands. This is a simple measure of psychological complexity, as it is more difficult for humans to understand longer pieces of text. But it’s far from clear that the length of an algorithm is a good measure of problem complexity, i.e. the complexity of the algorithm itself, without reference to how exactly it is implemented. The shortest possible algorithm to implement any given problem would at least contain the number of inputs, the number of outputs, and a function call to compute the output based on the inputs. Take for example the expression “y=f(x)”. In this expression, x is the input (e.g. a bank’s capital adequacy ratio), y is the output (e.g. whether or not the bank is solvent), and f is a function that determines whether a bank with given capital adequacy ratio is solvent or not.

Every algorithm must have at least one output and a number of inputs, and is implemented through a function f which can reference other functions to evaluate the output as a function of the inputs. So the potential volume (the complexity of the most abstract and high-level description) of an algorithm equals two plus the number of unique inputs. This measure is independent from how the function to compute the output is implemented and therefore the potential volume is a measure of problem complexity.

With this nomenclature we can now determine how close a given algorithm is to the shortest possible algorithm. We call the ratio of the potential volume over actual volume the level of the algorithm. If the level is high, it means that the regulation has a very specific vocabulary, a technical jargon opaque to outsiders. Conversely, a low level means that the regulation starts from elementary concepts and operations. In particular, a low level means that the representation of regulation defines auxiliary functions (operators) in terms of more elementary ones. Under this interpretation, we can see that there is a very intuitive trade-off between volume and level. It is possible to shorten the regulation by using a more specialized vocabulary, but this is going to increase the level and make the regulation more opaque. Conversely, one can make regulation more accessible or self-contained by defining the specialized words in terms of more elementary ones, but the cost is a greater length.

Proof of Concept – The Complexity of Basel I

We show how to measure the complexity of capital regulation in practice by considering the design of risk weights in the Basel I Accords. This is a nice testing ground because this part of the regulation is very close to being an actual algorithm. We compare two different methods: (i) We write computer code corresponding to the instructions of Basel I and measure the algorithmic complexity of this code, that is, we use the measures of algorithmic complexity literally; and (ii) We analyze the text of the regulation and classify words according to whether they correspond to what in an algorithm would be an operand or an operator, and compute the same measures, this time trying to adapt them from the realm of computer science to an actual text.

So, for example, the fact that the regulatory text “Claims on banks incorporated in the OECD and loans guaranteed by OECD incorporated banks” is in the 20% risk-weight category, translates into the following actual computer code:

We can easily identify the operands and operators in such a piece of code, and compute our measures of complexity. The operands in the code corresponding to Basel I are the different asset classes (e.g. ASSET_CLASS, claims), attributes (e.g. ISSUER_COUNTRY, GUARANTOR), values of those attributes (e.g. oecd, bank), and risk-weights (e.g., risk_weight, 0.2). The operators are if, and, or, else, ==, >, ≤, and !=.

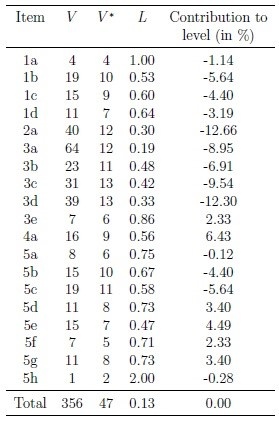
Given our algorithmic representation of Basel I, we find that there are 172 operators and 184 operands, of which 8 are unique operators and 45 are unique operands. To give sense to these numbers, we can go further by computing how much the regulation of a given asset class contributes to the total level of the regulation (see Figure 1). We obtain an item’s marginal contribution to complexity by computing the complexity of the entire Basel I regulation without the item. A positive marginal contribution means that the level of the item is higher than the average level of the remaining items. This helps us to understand which items increase the overall complexity of a regulation.

Figure 1: Marginal complexity of different parts of Basel I regulation
The numbering of the different items corresponds to the Annex 2 of the Basel I text (BCBS 1988). For each item we compute the volume V, the potential volume V*, and the level L. Finally, for each item we compute the level of the entire regulation with and without the item in order to compute the “contribution to level”. A positive number means that adding a given item to the rest of the regulation increases the total level.

The measures we obtain using both approaches are highly correlated, from which we conclude that our measures can be used without actually “translating” a regulatory text into a computer code, which is of course a time-consuming task, as they can be proxied by studying the text directly.

Application – Complexity of the Dodd-Frank Act

Given the encouraging results obtained with the Basel I Accords, we then turn to the question of how the Halstead measures can be computed at a much larger scale by applying our text analysis approach to the different titles of the 2010 Dodd-Frank Act. Because the Dodd-Frank Act covers many different aspects of financial regulation, when doing this analysis we created a large dictionary of operands and operators in financial regulation, as well as specialized software that helped us in manually classifying a large body of text.

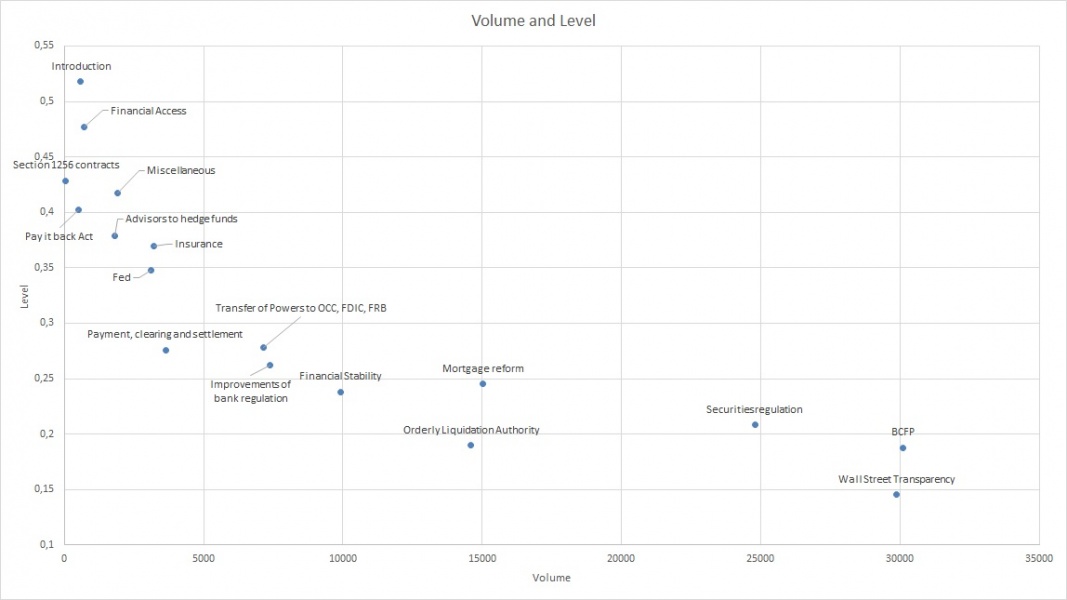
Our paper provides informative descriptive results on which titles are more complex according to different dimensions (see Figure 2). In particular, we note that some titles have approximately the same length and yet differ very significantly along other measures, which shows that our measures capture something different from the mere length of a text. Two titles with approximately the same volume (number of words classified as operators plus number of words classified as operands) can have very different levels, as can be seen from the titles “Introduction” and “Pay it back Act”. Both are about the same length, but the Introduction has a much higher level, likely because it introduces a number of high-level technical jargon not present in the “Pay it back Act” title.

Figure 2: Volume vs. Level of different sections of the Dodd-Frank Act
For each Title of the Dodd-Frank Act we compute the Volume and the Level. This figure gives a scatter plot with Volume on the X-axis and Level on the Y-axis.

The dictionary and the code to generate the classification software can be found online.2 Applying the same approach as before to the 16 Titles of the Dodd-Frank Act plus its introduction, our dictionary contains 667 unique operators (374 logical connectors and 293 regulatory operators), 16,474 unique operands (12,910 economic operands, 560 attributes, and 3,004 legal references), as well as 711 function words and 291 other, unclassified words. In other words, we classify 98.4% of the 18,143 unique words used in the Dodd-Frank Act.

Outlook: Is This How Humans Perceive Complexity?

The major open question that remains is whether our measures of complexity are indeed how humans perceive complexity. At the end of the day, this is what matters: do our measures capture what those who have to deal with regulations perceive as “complex”? To address this question, our paper describes an experimental protocol.

Experimental subjects are given a regulation consisting in (randomly generated)Basel-I type rules, and the balance sheet of a bank. They have to compute the capital ratio of a bank and say whether the bank satisfies the regulatory threshold. The power of a measure of regulatory complexity is given by its ability to forecast whether a subject returns a wrong value of the capital ratio, and the time taken to answer. Moreover, we can test whether the relation between the measure of regulatory complexity and the outcome depends on the student’s background and training, etc. Importantly, our protocol can be used to validate any measure of regulatory complexity based on the text of a regulation, not only ours, and thus opens the path to comparing the performance of different measures. Ultimately, the objective would be to establish a standard method to measure the power of a measure of complexity. This has been done in computer science, in which there is a literature testing whether different measures of algorithmic complexity correlate with mistakes made by the programmers or the time they need to code the program.

Conclusion

Our paper is only a first step in applying this new approach to the study of regulatory complexity, and is meant as a “proof of concept”. We show how some of the simplest measures of regulatory complexity can be applied to financial regulation in different contexts: (i) an algorithmic “translation” of the Basel I Accords; (ii) the original text of the Basel I Accords; (iii) the original text of the Dodd-Frank Act; and (iv) experiments using artificial “Basel-I like” regulatory instructions.

While the results we present are preliminary — for example we do not cover procedural rules with our approach — we believe they are encouraging and highlight several promising avenues for future research. First, the dictionary that we created will allow other interested researchers to compute various complexity measures for other regulatory texts and compare them to those we produced for Basel I and the Dodd-Frank Act. Moreover, the dictionary can be enriched in a collaborative way. Such a process would make the measures more robust over time and allow us to compare the complexity of different regulatory topics, different updates of the same regulation, different national implementations, etc. This can also serve as a useful benchmarking tool for policymakers drafting new regulations. Second, the conceptual framework and the experiments we propose to separate three dimensions of complexity (problem, psychological, computational) can be applied to other measures that have been proposed in the literature, so as to better understand what each one is capturing. Finally, our measures could be used in empirical studies aimed at testing the impact of regulatory complexity, and in particular testing some of the mechanisms that have been proposed in the theoretical literature.