Models of price setting and inflation dynamics: A summary

In a recent paper, we review models of nominal price adjustment based on optimizing or near-optimal behavior, including menu cost models, generalized hazard function models, and models of frictional decisions. We find that a variety of models in which the probability of price adjustment is a smoothly-increasing function of the retailer’s gains from adjusting the price can successfully explain both microeconomic evidence on retail price setting and macroeconomic evidence on the real effects of monetary policy surprises.

1. Models of price setting

Researchers seeking to understand inflation at the micro level must grapple with the fact that the nominal prices of most products in most sectors do not adjust smoothly over time. Instead, nominal prices are sticky – that is, a retailer typically holds the nominal price of any given product fixed over a substantial interval of time before adjusting it by a discrete amount1. Price stickiness is also crucial for macroeconomics, because it suggests that the economy does not exhibit monetary neutrality – that is, an increase in the money supply does not lead to a proportional rise in the prices of all goods and services that would leave real conditions unchanged. Instead, monetary stimulus causes some prices to adjust, while others remain the same, implying changes in relative prices and opening the door to possible effects on the real economy.

Indeed, econometric estimates suggest that looser monetary conditions stimulate real activity in a temporary but persistent way (see, for example, Christiano et al., 2005, and Smets and Wouters, 2003). Therefore, mainstream macroeconomic models used for economic policy guidance are built on the assumption of sticky nominal prices2. The framework most commonly used by applied macroeconomists for modelling price adjustment is that of Calvo (1983), who assumed that there is a constant probability λ of nominal adjustment in any given period, implying that the nominal price (or wage) remains fixed for T ≡1/λ periods, on average, between one adjustment and the next3.

However, over the past two decades, macroeconomists have sought to build models capable of reproducing observed patterns of price setting in retail microdata without losing sight of firms’ strong incentives to adjust prices optimally. The adjustment behavior in these microfounded models is often called state-dependent pricing (SDP), since optimization implies that the probability of repricing should change – in contrast to Calvo’s assumption – whenever the state of the aggregate economy or the firm’s own situation changes. In a recent paper, we have reviewed the current literature on SDP models of price setting4. We identify four main streams of literature on the microfoundations of nominal rigidity. First, some models assume a fixed cost for adjusting a product’s nominal price, often called a menu cost (MC). In a second class of models, the probability of resetting the nominal price is a smoothly increasing function of the value gained by adjusting, often called a generalized hazard function (GHF). Third, some models suppose that making accurate decisions is costly, either because the required information inputs are costly, or because the decision process itself has costs. These forms of costly managerial choice are one of the possible explanations for GHF behavior. Fourth, many papers emphasize real rigidities that can reinforce the impact of nominal rigidities.

Influential early papers suggested that macro models with SDP behavior might have very different implications for monetary policy. A key difference is that the aggregate price level reacts more quickly in menu cost models, compared with the Calvo model. This is because MC models display a selection effect: the products whose prices are currently too low are more likely to reprice in response to an inflationary shock than products whose prices are currently on target or too high. Golosov and Lucas (2007) quantified these issues in an MC model where firms faced product-specific productivity shocks. They found that after a surprise increase in money growth, the aggregate price level adjusts fully within a month or so. This quick transmission is driven by more frequent large price increases, and less frequent large price decreases (other sizes of price changes are not observed — see the top, right panel of Figure 1 for an illustration). In contrast, under the Calvo framework, an inflationary shock leaves the adjustment probability unchanged, and the products that do reprice are a random sample, so they are no more likely to require a large increase than those that fail to adjust. Hence the aggregate response of prices to a monetary stimulus is faster under menu costs (and therefore the response of real output is weaker), both due to the extensive margin – the increased fraction of prices adjusting – and due to the selection effect – the systematic correlation between the reset probability and the size of the desired change.

Figure 1. Effects of a positive money growth shock
Menu cost model (top row) versus generalized hazard function model (bottom row)

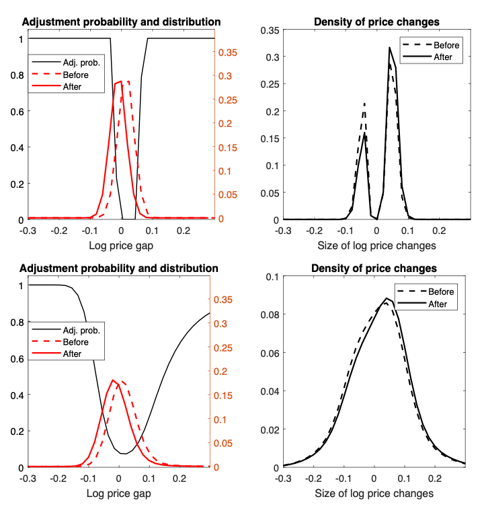
Left column: Distribution of log price gaps, before and after the shock, and adjustment probability as a function of the log price gap. Right column: Distribution of log price changes, before and after the shock.

2. Conclusions about inflation dynamics

In spite of the early impression that SDP models might revolutionize macro modelling, recent literature shows increasing consensus that the state-dependent models which match empirical patterns from microdata share many of the macro properties of the Calvo model. In retail microdata, price adjustments vary greatly in size – positive and negative and large and small price changes coexist, even after filtering out the ones related to “sales” (i.e. temporary price discounts). Also, studies that estimate the adjustment probability find a strictly positive, smoothly increasing function of the gap between the current price and the firm’s desired price, even when accounting for product-specific heterogeneity in repricing probabilities (see, for example, Campbell and Eden, 2014). These stylized facts are inconsistent with the sharp threshold behavior predicted by the basic MC model of Golosov and Lucas — in which the repricing probability jumps from zero to one as soon as a product’s price deviates sufficiently from its target value — and instead favor the smoother behavior of GHF models. The smooth adjustment in the GHF framework weakens the selection effect, as can be seen in the bottom row of Fig.1, where an increase in the money supply slightly raises the average price adjustment but has little impact on the shape of the price change distribution. Therefore, GHF models imply stronger real effects of monetary shocks than Golosov and Lucas (2007) found5.

Smoothly state-dependent adjustment may occur for a variety of reasons. First, if the cost of price adjustment is an i.i.d. random variable, instead of a fixed constant — that is, if we consider a stochastic menu cost instead of a fixed menu cost — then the firm may display smooth GHF adjustment behavior, as in Dotsey and Wolman (2020). Second, menu costs give rise to GHF adjustment when firms sell multiple products and face economies of scope in price setting, as in Midrigan (2011) and Alvarez and Lippi (2014), where a firm pays a single menu cost to reset the prices of all the products it sells. The adjustment decision then depends on the average gap between the firm’s prices and their target values, so when updates occur, some will be large (reflecting a large gap) and others will be small (reflecting a small gap). GHF adjustment can also be explained by costs associated with precise decision-making. In particular, if it is costly to control the timing of price setting with high accuracy, as in Woodford (2009), Alvarez et al. (2017), and Costain and Nakov (2019), then the probability of repricing will be a smooth function of the value of adjustment.

While various mechanisms can generate nominal rigidity, a number of recent papers have derived analytical relationships between the micro and macro behavior of sticky price models that are applicable quite generally across Calvo, MC, and GHF frameworks. A useful indicator of the variability of the sizes of price changes in microdata is the kurtosis of the price change distribution. When small and large price changes of both signs coexist, kurtosis is high, and the selection effect is weak. Hence it can be shown, across many models, that the cumulative impulse response of real output to a monetary shock is proportional to the kurtosis of the price change distribution and inversely proportional to the adjustment frequency (Alvarez et al., 2016). Likewise, recent equivalence results show that, to a first-order approximation, many state-dependent pricing models share the same aggregate dynamics as a Calvo model, as long as parameters are adjusted appropriately (Auclert et al., 2024; Alvarez et al., 2022). Besides the adjustment frequency and the kurtosis of the price change distribution, the third factor that is crucial for the real impact of a monetary shock is the degree of strategic complementarities between the choices of different price setters (Alvarez et al., 2023). Strategic complementarities between the prices of inputs and outputs (Costain et al., 2022; Auclert et al., 2024) or the prices of oligopolistic competitors (Mongey, 2021; Afrouzi, 2023) can both reinforce the real impact of monetary shocks.

Table 1. Matching real effects from SDP models with Calvo models

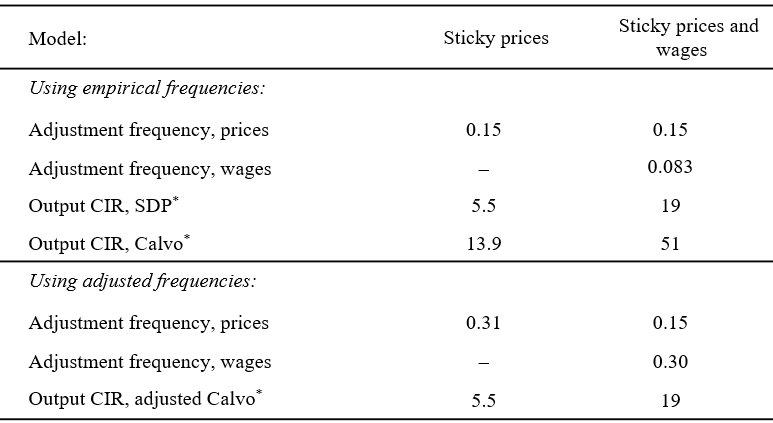
Top panel: SDP models are compared to Calvo models with the same monthly adjustment frequencies. Bottom panel: Monthly Calvo frequencies altered to produce the same cumulative impulse response (CIR) as the SDP models. * Note: The CIR refers to the area under the real output impulse response function, calculated at monthly frequency.

Table 1 quantifies the relationship between SDP and Calvo models by comparing the real effects of monetary shocks across the two frameworks. We report the CIR of real output in response to a 1% money supply growth shock with monthly autocorrelation 0.8, in GHF models with sticky prices on final goods only (Costain and Nakov, 2019), or with sticky prices on final goods and sticky wages for labor (Costain et al., 2022). Notice that the real effects are much larger (the output CIR rises from 5.5 to 19) when two layers of nominal stickiness interact. These models are calibrated to microdata on retail price changes (both columns) and on wage changes (last column), implying a monthly adjustment probability of 15% (8.3%) for prices (wages). The first panel of the table compares these SDP models to Calvo models with the same adjustment rates: the Calvo frameworks imply real effects 2.5 to 2.8 times greater than the smooth SDP models.6 The second panel asks how much the Calvo adjustment rate would have to be increased in order to produce the same real effects as the SDP setup. In the specifica-tion with sticky prices only, roughly doubling the adjustment rate, from 0.15 to 0.31 monthly, gives the same real impact as the SDP model. In the case with sticky prices and wages, we hold the price reset probability fixed, and find that the wage reset rate must roughly triple in the Calvo case – from 0.083 to 0.30 monthly – to give the same CIR as the SDP model.

In spite of the equivalence between SDP and Calvo models for approximating the impact of small shocks, state state-dependent models imply that price changes can be rapid and flexible when circumstances warrant. At very high inflation rates, the state state-dependent adjustment frequency rises in proportion to inflation, and the quantitative predictions of MC models fit data from hyperinflationary environments well (Alvarez et al., 2019). Likewise, sufficiently large macroeconomic shocks propagate quickly to prices, so their real impact is similar to what a flexible flexible-price model would imply (Karadi and Reiff, 2018; Cavallo et al., 2023). Similarly, since the adjustment frequency rises with inflation in SDP models, the Phillips curve becomes steeper at higher inflation rates (Costain et al., 2022; Afrouzi and Yang, 2021). Furthermore, the flexibility of SDP behavior – when necessary – reduces the welfare losses caused by frictions, because firms tend to adjust before their prices deviate from target by an especially costly amount. This reduces the welfare costs of inflation in SDP models, compared with the Calvo and Taylor frameworks. Hence, while Schmitt-Grohé and Uribe (2004) found that optimal steady-state inflation is state inflation is very close to zero in a Calvo model, recent analyses find higher optimal inflation rates. Adam and Weber (2019) find an optimal inflation rate of 1% per annum, due to idiosyncratic productivity trends in a model of product  turnover, while Blanco (2021) calculates an optimal rate of 3.5% per annum due to the lower welfare costs of inflation under SDP.

Staggered adjustment driven by menu costs or Calvo frictions helps explain why the aggregate price level is sluggish, but does not, on its own, explain why the inflation rate is persistent. These frameworks are entirely forward-looking, so they slow the convergence of the price level after an aggregate shock, but the adjustment begins as soon as the shock hits. Hence even though prices are sluggish, the inflation rate jumps immediately after a shock, unless it is held back by some institutional constraints such as indexation of wages or prices (Galí et al., 2005). However, strategic complementarities and frictions in information flow can help explain the sluggishness of the inflation rate, as well as that of prices. Strategic complementarities can magnify the stickiness of prices, and if they are sufficiently strong they can also make the inflation rate persistent, giving rise to a hump-shaped inflation response to a monetary shock (Alvarez et al., 2023). In particular, strategic complementarities in price setting in input-output networks enhance inflation persistence under many types of nominal frictions, as inflationary shocks filter gradually from primary inputs to final goods retail prices. Similarly, frictions relating to information flow – including “rational inattention” (Sims 2003) and related frameworks – can stop news about aggregate shocks from filtering immediately into price and wage setting decisions, making the inflation rate sluggish too (Mankiw and Reis, 2002; Woodford, 2003; Mackowiak and Wiederholt, 2009; Afrouzi and Yang, 2021).