Monetary policy space and monetary policy strategies for the euro area

We analyze the economic performance of different monetary policy strategies, or rules, in a low interest rate environment, using simulations with a DSGE model which has been estimated for the euro area. We present three sets of results. First, the macroeconomic costs of the effective lower bound of interest rates (ELB) are likely to grow in a non-linear manner if the monetary policy space (the difference between the normal, or average, level of nominal interest rates and the ELB) shrinks. Second, the (relative) performance of low-for-long (L4L) monetary policy rules depends on the size of the monetary policy space. The L4L rules tend to perform well, if the monetary space is small, but if the space is larger these rules, while stabilizing inflation, may lead to more volatility in the real economy than flexible inflation targeting. Third, a point inflation target appears to outperform a target range.

Recently monetary policy strategies have been under review in the euro area as well as in several other economies and central banks.2 An important motivation behind these strategy reviews has been the observation that interest rates have been falling over the past decades. As a result, it has become more likely that monetary policy is constrained by the effective lower bound of interest rates. To (re)express the situation facing many central banks in slightly different terms, one can say that the central banks’ monetary policy space has contracted. By the term ‘monetary policy space’ we refer to the distance between typical, or average, (short run riskless) nominal interest rates and the effective lower bound.

While many central bankers and macro economists tend to think that the diagnosis of a shrinking monetary policy space is likely to be correct, it is perhaps less clear how much the policy space has contracted, and how wide or narrow the space is currently in the euro area. This is a key starting point of our recent work (Haavio and Laine 20213). Using stochastic simulations with a structural macro (DSGE) model which has been estimated for the euro area, we analyze and compare the economic performance of different monetary policy strategies, or rules, in a low interest rate environment. Our major aim is to study how the (relative) performance of the rules depends on the monetary policy space.

The model framework we use involves several frictions and market imperfections, which are empirically realistic, and important for the analysis of monetary policy. These frictions include sticky prices and wages, as well as financial frictions. Note that unlike in the simplest possible – or canonical – New Keynesian models, in our framework with multiple frictions (as well as shocks) the ’divine coincidence’ does not hold. Hence, there is typically a trade-off between stabilizing inflation and the real side of the economy.

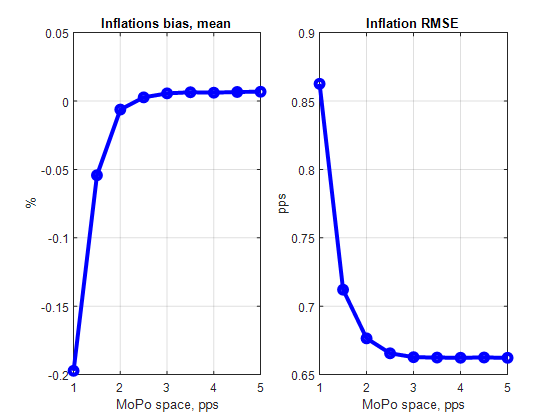
We establish three sets of results. The first set of results suggests that the macroeconomic costs of the effective lower bound grow in a non-linear manner when the monetary policy space shrinks. The effective lower bound (ELB) binds more frequently, and the episodes when interest rate are at effective lower bound become longer. The volatility of real activity, unemployment and inflation increases; the downward bias in inflation becomes more pronounced, the average unemployment rate rises, and the output gap becomes more negative on average. If the monetary policy space shrinks from 4 percentage points to 3 percentage points, our simulations suggest that the macroeconomic dynamics may not change that much. However, if the monetary policy space further shrinks from 3 to 2 percentage points, and perhaps even further to 1 percentage point, the induced increase in macro volatility can be much more substantial. See Figures 1 and 2.

Figure 1. Monetary policy space and macroeconomic outcomes under baseline monetary policy rule: The real economy.

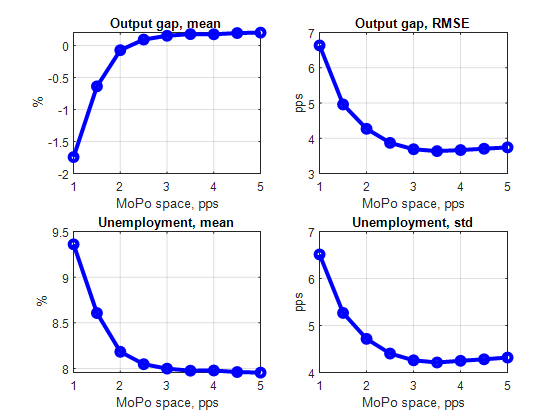
Figure 2. Monetary policy space and macroeconomic outcomes under baseline monetary policy rule: Inflation.

Second, we compare our estimated baseline monetary policy rule to a number of different make-up strategies, or low-for-long (L4L) monetary policy rules. Our estimated baseline is a Taylor-type flexible inflation targeting rule which involves interest rate smoothing; according to the rule the central bank reacts to one-year-ahead expected inflation, as well as to a measure of the output gap and to a measure of the natural rate of interest.4 The general idea of make-up strategies is to compensate for the accommodation that is forgone due to the ELB. Specifically, we consider flexible price level targeting, average inflation targeting and temporary price level targeting. Flexible price level targeting means that the central bank reacts to deviations of the price level from its trend (e.g. 2 % annual growth). By average inflation targeting we mean that the central bank reacts to the deviations of average past medium-term inflation from the inflation target. Hence, if during an ELB episode realized inflation falls short of the inflation target, flexible price level targeting and average inflation targeting imply a de facto commitment to keep interest rate low for long, even after the economy starts recovering and (current) inflation picks up. Finally, temporary price level targeting means that policy makers commit to deferring interest rate increase at least until any shortfall in inflation over the entire ELB period is fully made up. Away from the ELB, the central bank follows the baseline Taylor rule.

Our results suggest that the make-up strategies may alleviate the problems caused by the ELB. However, we also find that the (relative) performance of the L4L rules depends on the size of the monetary policy space. These rules tend to perform well, relative to the baseline flexible inflation targeting rule, if the monetary policy space is small. Under these circumstances the ELB constitutes a truly serious constraint to monetary policy and the accommodation provided by make-up strategies is highly useful. But if the monetary policy space is larger, the L4L rules, if mechanically followed, may result in more volatility in the real economy, while stabilizing inflation.

Third, and finally, we compare two possible definitions of price stability. The first definition, or operationalization, of price stability is a point inflation aim, say 2 % annual inflation. While many central banks do in fact define price stability in terms of a point inflation target, this is not the only possible option. For example, the Eurosystem’s definition of price stability, medium run inflation below, but close to 2%, is not (de jure) a point target. The second possible definition, or operationalization, of price stability that we analyze is an inflation target range. The idea is that the central bank does not aim at a point target, but it has a range of values for inflation – say from 1% to 2% – that it considers to be consistent with its definition of price stability. To be more specific, we assume in the simulations that if inflation is within the target range, the central bank reacts less strongly to changes in inflation, while it can also seek to stabilize the real economy. For the ECB this is a part of the secondary objective of monetary policy. When inflation is outside the target range the central bank follows the baseline Taylor rule – unless the ELB binds.

Overall, our results suggest that a point inflation aim outperforms an inflation target range. Both alternatives tend to generate similar results for the real economy – measured by the level and volatility of output and unemployment. However, the target range definition of price stability gives rise to more volatile inflation.