Optimal timing of environmental policy under partial information

This policy brief summarises the key insights found in Garcia (2024). There I explore the optimal timing of environmental policy when the stock of natural capital, which follows a stochastic process, is imperfectly measured. The decision-maker must therefore infer it by combining a noisy signal with her own past beliefs. I present two key insights. First, noisy signals about the natural capital stock blur the inference process, thereby easing the conditions under which policy adoption becomes optimal. Second, the interaction between natural capital stock volatility and the inference process gives rise to new effects that are absent under perfect information. Specifically, the impact of increased volatility on the conditions for optimal policy adoption varies depending on the information set. My work contributes to both the environmental policy timing literature and the field of resource management under incomplete information.

Overview

When should society implement a costly policy to safeguard the environment? In his seminal works, Pindyck (2000, 2002) addresses this question using the real option theory. In his setup, environmental quality follows a stochastic process with a downward trend. A decision-maker must then choose the optimal time to enact a policy that safeguards the environment, but incurs economic costs. He analyses how structural factors, such as environmental volatility and the discount rate, affect the timing of environmental policy.

Pindyck’s work relies on a strong assumption: full information. The controller perfectly observes environmental quality at each instant. In reality, however, measuring something as complex as natural capital (or its inverse, environmental degradation) is hard; there is no simple, granular, universal metric. Hence, policy makers often monitor different indicators to understand how natural capital stocks are changing around the world (Dasgupta, 2021).

To illustrate, the Living Planet Index (LPI) measures the state of global biodiversity by tracking thousands of population trends of vertebrate species. Widely used by conservationists and policymakers, the index was, for example, adopted by the Convention on Biological Diversity as an indicator of progress towards its target to ‘take effective and urgent action to halt the loss of biodiversity’. As shown in Figure 1, however, significant uncertainty surrounds the index. These wide confidence bands, a recurring feature in biodiversity indicators, highlight the challenges of measuring natural capital stocks.

Figure 1: Living Planet Index

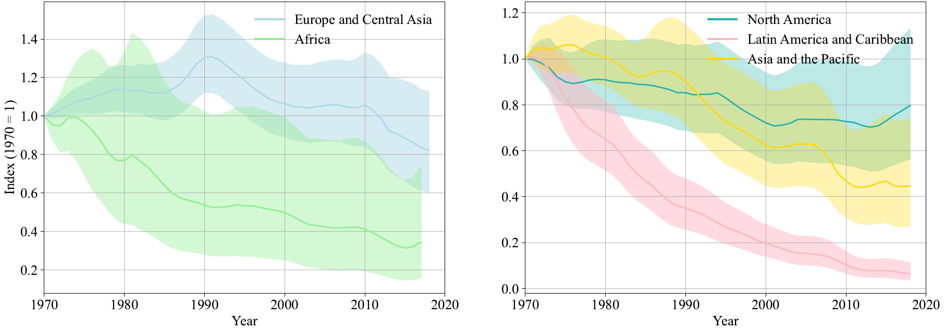
Notes: The Living Planet Index measures the state of global biological diversity based on population trends of vertebrate species from terrestrial, freshwater and marine habitats. Bold lines show index values and shaded areas represent statistical certainty surrounding the trends (95%). The Living Planet Index is maintained by the World Wildlife Fund and the Zoological Society of London.

Partial information affects the optimal timing of environmental policy

My work relaxes the full information assumption. Instead, it presents an optimal stopping problem under partial information. This still assumes a stochastic process with a negative drift for the stock of natural capital. A controller must choose the optimal time to implement a policy that permanently freezes the natural capital stock at its current level. However, implementing the policy is costly, for it has a negative impact on the reward function. The novel modelling feature is that the controller does not observe the stock of natural capital; that is, she faces ignorance uncertainty (Tsur and Zemel, 2014). She must therefore infer the level of the natural capital stock by combining a noisy signal with her own past beliefs.

A simple example helps to illustrate the rationale of my work. A policymaker is responsible for safeguarding a fragile ecosystem susceptible to unpredictable shocks, like weather changes affecting the outburst of a pollution-induced disease. Specifically, her task is to determine the right moment to implement a conservation policy that preserves the ecosystem at its current state. In making this decision, she faces two challenges. First, adopting the policy involves economic costs, such as job losses and stranded assets. Second, the ecosystem’s fragility is not known with certainty, and can only be imperfectly measured.

To fix ideas, I begin by analysing a full information setup, where the controller perfectly observe the stock of natural capital. Here it is optimal to adopt the conservation policy as soon as the natural capital stock exceeds an endogenous threshold. The left panel of Figure 2 illustrates this optimal stopping strategy, depicting the three possible alternatives: immediate policy adoption, policy adoption at some future date, or no policy adoption at all.

Figure 2: Graphical illustration of the optimal adoption strategy

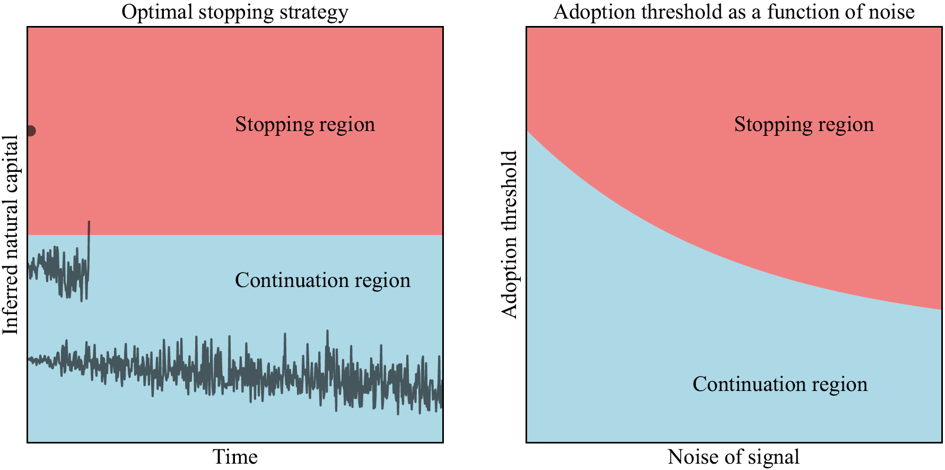
Notes: It is optimal to adopt the environmental policy as soon as the inferred natural capital stock enters the stopping region. Under full information, the controller’s beliefs coincide with reality.

To better understand this finding, consider the analogy of selling an asset with a fluctuating price. Selling only becomes optimal when the price of the asset is high (see e.g. Oksendal, 2003). The same logic applies here. Because the reward function depends on the natural capital stock at the time the policy is adopted, the controller waits for favourable realisations of the natural capital stock. The structural parameters of the model give the word favourable its meaning.

Suppose now the controller faces ignorance uncertainty and must infer the natural capital stock by combining a noisy signal with her own past beliefs. My work conveys two key messages. First, a noisy signal about the current natural capital stock eases the conditions under which policy adoption becomes optimal. As mentioned earlier, policy adoption becomes optimal as soon as the inferred natural capital stock exceeds an endogenous threshold. As seen in the right panel of Figure 2, the noisier the signal, the lower the threshold. The intuition is straightforward. Noise blurs the inference process, prompting the controller to lower the policy adoption threshold in an attempt to mitigate the deterministic decline in the natural capital stock.

The second key message is that the interaction between the inherent volatility of the natural capital stock and the inference process gives rise to new effects that are absent in the full information baseline. Specifically, my model suggests divergent effects of high environmental volatility on the optimal policy adoption strategy when compared to the full information benchmark. This occurs because, under partial information, increased volatility heightens the uncertainty surrounding the inference process, a channel that is not present under full information. For instance, in a full information context, my model often suggests that greater environmental volatility leads to higher adoption thresholds, as in Pindyck (2000, 2002). However, partial information can reverse this effect, actually leading to lower thresholds.

Avenues for future research

In reality, most environmental measures are not all-or-nothing decisions; they can be continuously adjusted post-adoption. Therefore, jointly considering the optimal adoption timing and the intensity of environmental measures under partial information is a fruitful avenue for future research.