

The views expressed here are those of the authors and do not necessarily reflect those of the Federal Reserve Bank of San Francisco or the Federal Reserve System.
The real interest rate consistent with stable inflation—the natural rate of interest—has displayed a sustained downward trend in advanced economies over the past decades. Over the same time period, the volatility of housing prices has increased considerably. In this Brief, we show that these phenomena are connected and have implications for optimal monetary policy. Embedding housing price growth extrapolation, consistent with survey data evidence, into a sticky price model with a lower-bound constraint on nominal interest rates, we show that lower natural rates of interest increase the volatility of housing prices and thereby also the volatility of the natural rate of interest. This exacerbates the relevance of the lower-bound constraint and causes the optimal inflation target to increase strongly with a decline in the natural rate of interest.
The natural rate of interest, i.e., the real interest rate on safe assets consistent with a stable inflation rate, has fallen significantly in advanced economies over recent decades. While the estimated levels of the natural rate vary across different estimation approaches, there is widespread agreement about the fact that their levels have featured a downward trend. Panel (a) of Figure 1 illustrates this trend using the estimates of Holston et al. (2017) and Fujiwara et al. (2016). Over the same time period of falling natural rates of interest, advanced economies have experienced a considerable increase in the volatility of housing prices, as shown by panel (b) of Figure 2.
In a recent paper (Adam, Pfauti, and Reinelt, forthcoming), we show that low natural rates of interest amplify the volatility of housing prices when households’ subjective housing price expectations are extrapolative. We show that in a sticky price model, this increases the volatility of the natural rate of interest, exacerbating the relevance of the lower bound constraint on nominal interest rates and causing Ramsey optimal inflation to increase strongly with a decline in the natural rate of interest.
Figure 1. Natural rates of interest in advanced economies (in %) and volatility of the price-to-rent ratio pre- and post-1990
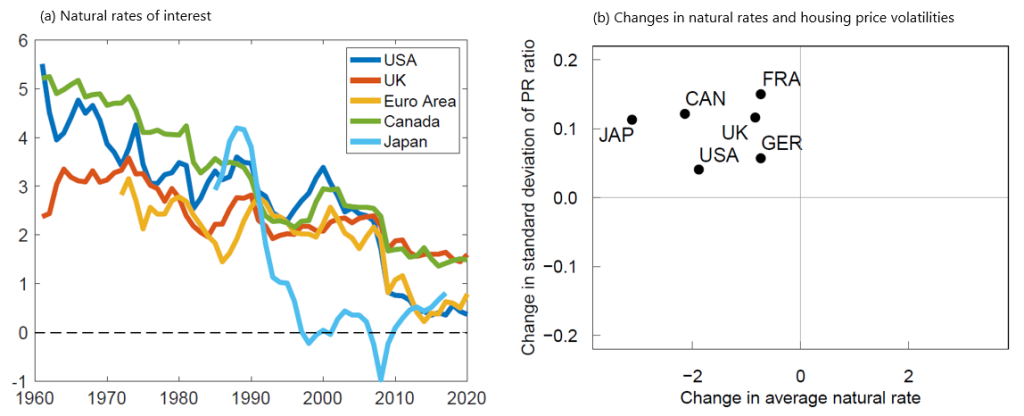
Notes: Panel (a) shows the evolution of the natural rate of interest taken from Holston et al. (2017) and Fujiwara et al. (2016). Panel (b) plots the pre-/post-1990 changes in the Holston et al. (2017) average natural rate, against the changes in the volatility of the price-to-rent ratio for different advanced economies. The sample period is 1970Q1 to 2020Q2. Volatility is defined as the standard deviation (pre-/post-1990 periods) relative to the period-specific mean value.
We comprehensively quantify the dimensions along which households’ housing price expectations deviate from the full-information rational expectations benchmark. We do so using a single data set, so as to establish a coherent set of quantitative targets for our structural equilibrium model with subjective housing price expectations. We measure households’ expectations about housing price growth using the Michigan household survey. The survey provides subjective expectations about nominal four-quarter-ahead housing price growth for the period 2007-2021.
Our findings reveal three key dimensions in which household expectations deviate from full-information rational expectations. First, expectations about future housing prices exhibit sluggish updating over time. We show this by following the approach of Coibion and Gorodnichenko (2015), which relates households’ ex-post forecast errors about the future housing price level to their current revision in the four-quarter-ahead expected housing price. Under the full-information rational expectations hypothesis, information that is contained in agents’ information set, such as past forecasts, should not predict future forecast errors. We find, inconsistent with this hypothesis, that there is a positive and statistically significant relationship. This implies that housing price expectations are updated too sluggishly: when updating their expectations upwards (downwards), households on average underpredict (overpredict) the level of future housing prices. The magnitude of the estimates is also large in economic terms: forecast revisions should approximately be three times as strong as they actually are.
Second, we show that households’ expectations about housing price growth covary positively with current market valuation, as measured by the price-to-rent ratio, while actual future housing price growth covaries negatively with current market valuation. This pattern is akin to the one found for stock markets by Adam, Marcet, and Beutel (2017). Our results imply that a two standard deviation increase of the price-to-rent ratio by 15.5 units increases the mean household expectations about four-quarter-ahead real housing price growth by around 0.5%. Actual four-quarter ahead housing price growth, however, falls by around 1.5%, so that the forecast error is approximately 2%.
Third, we show that households initially underreact to observed housing price growth, i.e., are too pessimistic in the first few quarters, but later overreact and exhibit—after approximately twelve quarters—overly optimistic expectations. This exercise provides a unified assessment of the previous two findings: While the first result shows that households update short-term housing price beliefs on average too sluggishly, the second result indicates over-optimism when the current market valuation is high, which points to some form of overreaction to past housing price increases. It turns out that both patterns can be jointly understood by considering the dynamic response of actual and expected housing price growth to housing price changes. We investigate the dynamic response of households’ forecast errors about housing price growth in response to realized housing price growth following the approach in Angeletos, Huo, and Sastry (2020). Figure 2 shows the dynamic response of forecast errors to realized housing price growth. Forecast errors are initially positive but later on become negative before eventually disappearing. The positive values in the initial periods indicate that agents’ expectations react too sluggishly: realized housing price growth is persistently larger than expected. This implies that initially, expectations underreact to the observed change in housing prices. Subsequently, when housing price growth has fully materialized and housing prices plateau, agents are still optimistic about future housing price growth, thereby overestimating future housing price growth. This is consistent with the fact that housing price growth expectations display the wrong cyclicality with housing market valuation. It also implies that households miss the mean-reversion in housing price growth: forecast errors turn negative once housing prices stop increasing, with the negative forecast errors disappearing only slowly over time.
Figure 2. Dynamic response of households’ forecast errors about housing prices (in %) in response to a housing price innovation
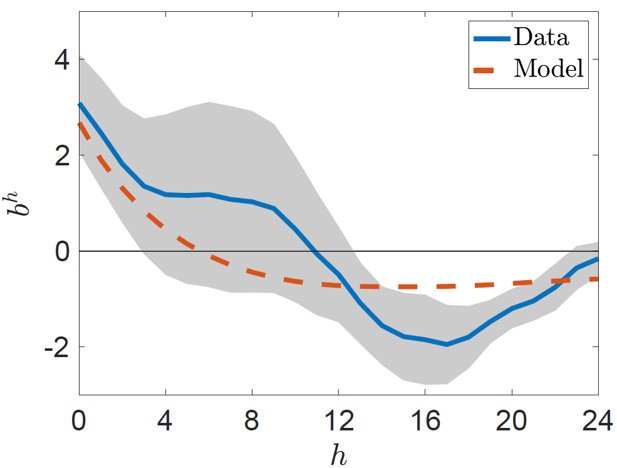
Notes: This figure reports the dynamic response of housing price forecast errors of one-year-ahead expectations to a one standard deviation innovation in housing price growth. The blue line represents the empirically estimated response. The red line represents the response in the model. Positive (negative) values indicate that realized housing price growth exceeds (falls short of) expected housing price growth. The shaded area indicates 90% confidence intervals.
We construct and calibrate a simple housing model with optimizing households and Bayesian belief updating, giving rise to extrapolative expectations about housing price growth. The model reproduces—as an equilibrium outcome—the three deviations of households’ beliefs from full-information rational expectations described above. For instance, the red dashed line in Figure 2 shows that the simple model matches the dynamic response of forecast errors about housing prices as estimated in the data. The ability of the model to account for these pat-terns in the data is a unique success of extrapolative beliefs: the model-based statistics would be identically equal to zero for a rational expectations model. Moreover, the model captures important patterns of the behavior of U.S. housing prices. Table 1 shows that subjective beliefs help substantially to explain the observed volatility in the price-to-rent ratio, volatility in housing price growth, and the strong autocorrelation in housing price growth. In contrast, a setting with rational housing price expectations is unable to jointly match these features of housing prices.
The simple model further shows that the effects of subjective housing price beliefs on equilibrium housing price dynamics are stronger in a low-rate environment, i.e., housing prices become more volatile when the natural rate of interest is lower. Panel (a) in Figure 3 depicts the model-implied relationship between the natural rate and the volatility of the price-to-rent ratio. This shows that lower natural rates are associated with larger housing price volatility, with the effect becoming quite non-linear for low levels of the natural rate. Consistent with this prediction, several advanced economies, including the United States, have experienced—concurrently with a decline in the natural rate of interest—a considerable rise in housing price volatility, consistent with panel (b) of Figure 1 above.
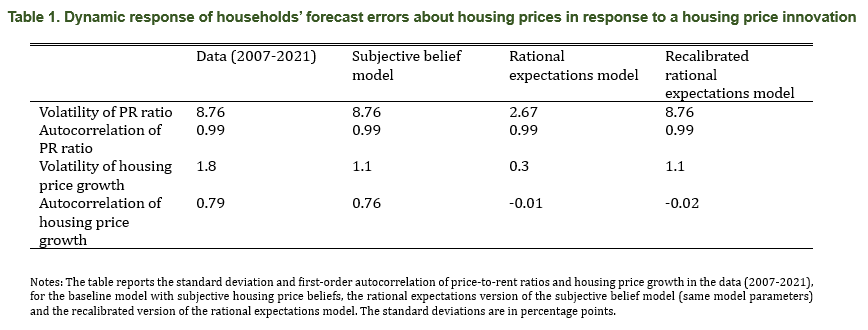
Figure 3. Volatility of the price-to-rent ratio given the level of the natural rate in the model
We analyze the monetary policy implications associated with subjective housing price beliefs and the resulting housing price dynamics by introducing housing price extrapolation into a New Keynesian model featuring a housing sector and a lower bound constraint on nominal interest rates. This full general equilibrium model quantitatively replicates the behavior of housing prices and the patterns of deviations from rational housing price beliefs. To allow for a meaningful examination of monetary policy in the presence of subjective beliefs, subjective housing beliefs are introduced in a manner that prevents monetary policy from manipulating household beliefs to its advantage.
We show analytically that the presence of subjective beliefs gives rise to housing price gaps, i.e., to deviations of housing prices from their efficient level, and that these housing price gaps have two important macroeconomic effects. First, a positive housing price gap, i.e., an inefficiently high housing price, makes it optimal for households to allocate more resources toward housing investment. For a given level of output, this depresses private consumption and thereby real wages, which manifests itself as a negative cost-push term in the Phillips curve. Second, a positive housing price gap also exerts positive pressure on the equilibrium output gap. When policy seeks to keep the output gap stable, it must implement higher (lower) real interest rates than in a setting with rational expectations, whenever the housing price gap is expected to increase (decrease). Since housing price gaps become more volatile when the average natural rate of interest is low, this feature implies that the volatility of the natural rate increases when the average level of the natural rate falls.
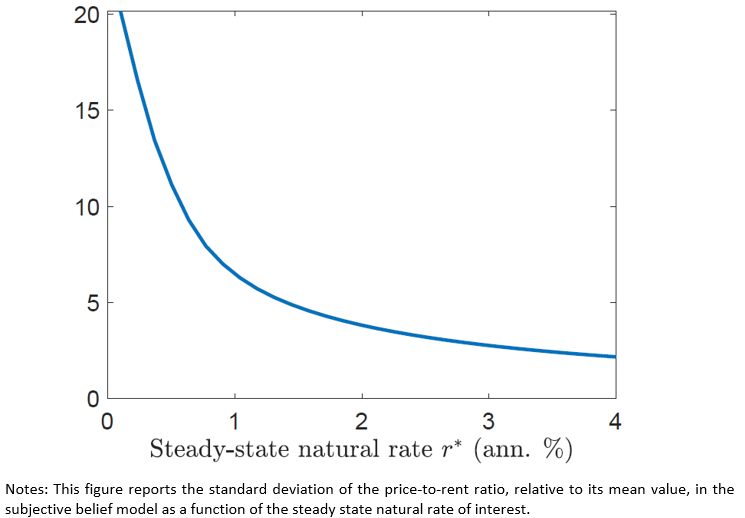
The fact that a lower average level of the natural rate also implies more natural rate volatility dramatically exacerbates the lower-bound problem for monetary policy. A more restrictive lower bound forces monetary policy to rely more heavily on promising future inflation to lower the real interest rate. Consequently, the optimal inflation target increases considerably as the average natural rate falls. Figure 4 depicts the optimal inflation target for different steady-state levels of the natural rate of interest. The figure graphs the optimal target for the setup with subjective housing beliefs (upper solid line), for the case with rational expectations (RE) about housing prices (lower solid line), and for a third case (dashed line) where housing price expectations are rational but the volatility of the natural rate increases exogenously as under subjective beliefs. We find that the optimal inflation target increases by approximately one-third of a percentage point in response to a one percentage point decline in the natural rate, with the increase being non-linear and becoming stronger for very low levels of the natural rate. In contrast, under rational expectations, the optimal inflation target is nearly invariant to the average level of the natural rate, because the volatility of the natural rate does not increase as its average level falls.
We also show that monetary policy should lean against housing price fluctuations induced by housing demand shocks, with reactions to housing price increases being more forceful than the reaction to housing price down-turns. None of these features is optimal if households hold rational housing price expectations. This highlights the importance of basing policy advice on economic models featuring empirically plausible specifications for household beliefs.
Figure 4. Average inflation under optimal monetary policy
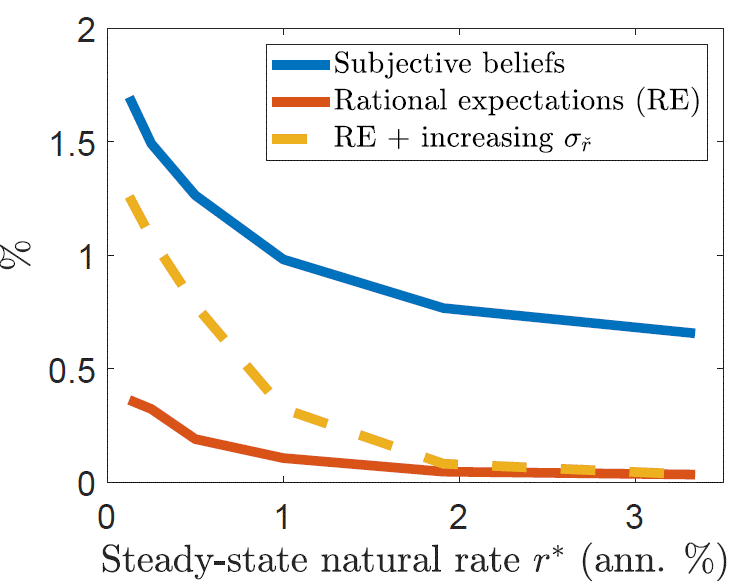
Notes: This figure reports the optimal inflation target for different levels of the steady-state natural rate in the presence of a zero low-er bound constraint. The red line shows the optimal target for the case with rational housing price beliefs and the blue line the one with subjective housing price beliefs. The yellow line shows the optimal average inflation under RE where the exogenous volatility of the natural rate is adjusted such that it matches the endogenous volatility increase under subjective beliefs.
Adam, K., A. Marcet, and J. Beutel (2017): “Stock Price Booms and Expected Capital Gains,” Amercian Economic Review, Vol. 107 No. 8, 2352–2408.
Adam, K., O. Pfäuti and T. Reinelt (forthcoming): “Subjective Housing Price Expectations, Falling Natural Rates, and the Optimal Inflation Target,“ Journal of Monetary Economics.
Angeletos, G.-M., Z. Huo, and K. A. Sastry (2020): “Imperfect Macroeconomic Expectations: Evidence and Theory,” in NBER Macroeconomics Annual 2020, Vol. 35.
Coibion, O. and Y. Gorodnichenko (2015): “Information Rigidity and the Expectations Formation Process: A Simple Framework and New Facts,” American Economic Review, 105, 2644–78.
Fujiwara, S., Y. Iwasaki, I. Muto, K. Nishizaki, and N. Sudo (2016): “Developments in the Natural Rate of Interest in Japan,” Bank of Japan Review.
Holston, K., T. Laubach, and J. C. Williams (2017): “Measuring the natural rate of interest: International trends and determinants,” Journal of International Economics, 108, S59 – S75, 39th Annual NBER International Seminar on Macroeconomics.