The paper provides a disaggregated mixed frequency framework for the estimation of GDP. The GDP is disaggregated into components that can be forecasted based on information available at higher sampling frequency; i.e. monthly, weekly or daily. The model framework is applied for Greek GDP nowcasting. The results provide evidence that the more accurate nowcasting estimations require i) the disaggregation of GDP, ii) the use of a multilayer mixed frequency framework, iii) the inclusion of financial information on a daily frequency. The simulation study provides evidence in favor of the disaggregation into components despite the inclusion of multiple sources of forecast errors.
Regarding the Greek GDP, there are not any models that incorporate recent econometric advances of GDP nowcasting. This paper fills this gap and provides a disaggregated mixed frequency framework for the estimation of Greek GDP.
The Greek GDP is disaggregated into components that can be forecasted based on information available at higher sampling frequency; i.e. monthly, weekly or daily. In the disaggregated approach, we nowcast each GDP component separately and aggregate them to obtain a GDP nowcast. We propose the estimation of GDP in constant prices according to the fixed-based approach, by nowcasting the components of GDP from the expenditure side. Hence, we define one model for each one of the components: private consumption of goods and services, government spending on public goods and services, investment in business capital goods, exports of goods, exports of services, imports of goods, imports of services and changes in inventories.
The proposed model has a multilayer framework. In the first layer, we estimate a mixed frequency regression for each GDP component, in which the dependent variable (e.g. growth in private consumption) is observed on a quarterly basis while the explanatory variables are observed on a monthly frequency. However, some of the explanatory monthly variables are published with a lag of several months, resulting in the unavailability of their most recent values. So, in the second layer of the model, we estimate the unavailable values of the monthly variables based on the information that is available at a higher frequency (i.e. daily frequency). For example, asset prices (e.g. stock prices) which are observed on a daily basis could provide information that is not incorporated in a monthly economic index (i.e. consumer confidence).
Moreover, we provide simulated evidence that more accurate nowcasting estimations require the use of a disaggregated multilayer mixed frequency framework. First, we show that the nowcasting ability of the AR(1) used as a naïve model is not better, if and only if a sophisticated model framework is defined. Second, the disaggregation into components reduces the nowcasting error despite the inclusion of multiple sources of nowcasting errors. Additionally, we provide a set of simulations, which help us to conclude that the aggregation of the predictions provides more accurate one-step-ahead predictions, despite the inclusion of multiple sources of forecast errors.
Overall, the results provide evidence that the more accurate nowcasting estimations require i) the disaggregation of GDP, ii) the use of a multilayer mixed frequency framework, iii) the inclusion of financial information on a daily frequency.
The proposed model framework, named D-model, is very relevant for practitioners and policymakers who need to get informed accurately and in real time of the current state of the economy under investigation. We would like to mention that the estimation of the D-model with the same structure among data and the same equations across layers but with data coming from another country will be like putting data into a black box. The construction of such a framework requires the knowledge of data availability, their quality and their interconnectedness. Thus, before the replication of the proposed model framework, the careful collection of the data and the construction of the appropriate connections among economic variables and across time, is a necessity.
|
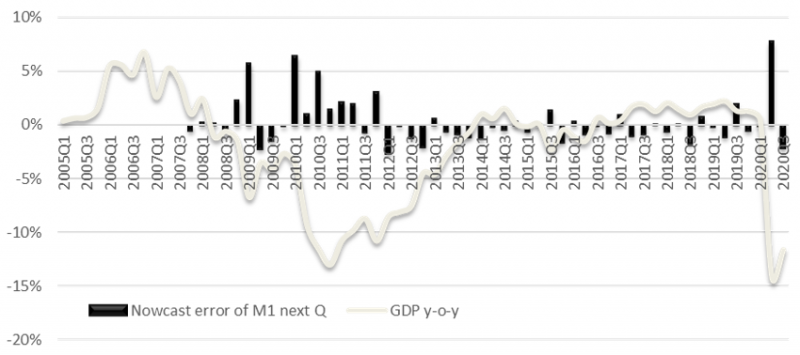
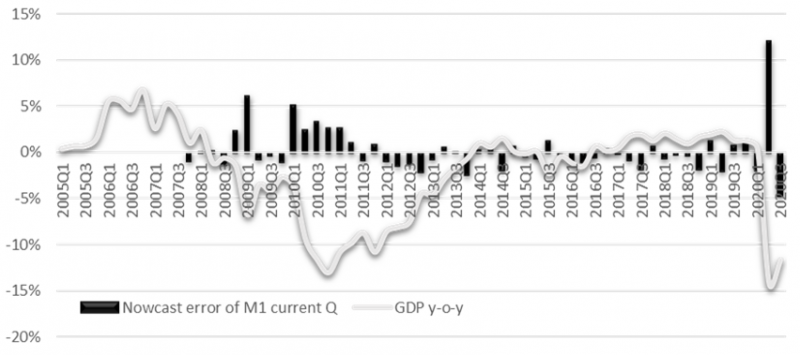
Figure 1 plots the y-o-y growth rate of GDP against the y-o-y nowcasting error. Naturally, there is a positive relationship between the magnitude of the growth rate and the nowcasting error. Moreover, we observe that the majority of the nowcasting errors are positive (mainly in the estimation based on the data available in the 1st month of the current quarter). This positive bias of the nowcasting errors indicates an autocorrelated error structure, which justifies the use of the nowcasting error correction. The unconditional correlation between y-o-y GDP growth and the y-o-y nowcasting error ranges from -48% (for M1 of next quarter) up to -62% (for M2 of next quarter). |
Figure 1: The GDP y-o-y growth rate and the relative y-o-y nowcasting errors of the disaggregated Midas model with the nowcasting error correction
The nowcasting error based on the data that are available up to the 1st month of the current quarter.
The nowcasting error based on the data that are available up to the 1st month of the next quarter.