The Political Economy of Currency Unions

How can a currency union be sustained when member states have an exit option? This paper derives how fiscal and monetary policies can ensure the survival of a common currency, if countries want to leave the union. A union-wide central bank can prevent a break-up by setting interest rates in favor of the country that wants to exit. I show how a central bank does this by following a monetary rule with state-dependent country weights. The paper then demonstrates in a simulation that a central bank can only sustain the union for a while with this rule, but not permanently and that the best way to sustain the union is through fiscal transfers.

Currency unions, such as the eurozone, may suffer instability if their membership is not seen as irrevocable. Even though the Treaty does not foresee exiting the euro, the eurozone sovereign debt crisis has forcefully shown that the possibility of a break-up was not fully ruled out. Indeed, markets have priced-in the risk of currency devaluations. Those risks are still present today and flame up during times of a crisis, as seen by increasing spreads of government bonds in the beginning of the covid crisis. Next to fiscal policy, the role of the European Central Bank for the currency union has been debated extensively. This poses the question what monetary policy can actually do if the threat of a break-up confronts the union. How can a central bank help to make a currency union sustainable? Should it do “whatever it takes” to preserve the common currency- and if so how?

To answer this question, I derive optimal fiscal and monetary policies for a currency union with exit option. I use an open economy model with different monetary regimes and run a simulation in which the union is subject to asymmetric shocks. These simulations are considered under different policy rules, such as fiscal policy under exit options and optimal monetary policy that reacts to the threat of an exit as well. Running the same simulations under different policies, one can assess the outcome of the effectiveness of those policies by checking how long the currency union survives. I find that the central bank can indeed extend the lifetime of a currency union by accommodating relatively small asymmetric shocks. It does that by putting more weight on the country that would otherwise leave the union. The ability of the central bank to sustain the union over a longer time horizon is however limited, as monetary policy is an inefficient tool to favor specific countries. If large shocks hit the union, monetary policy will not have enough firepower to redistribute a sufficient amount of resources across the union to prevent a break-up. In those situations, in which monetary policy falls short, other means are needed to sustain the union. I show that fiscal policy is capable to preserve the currency union for a long time horizon – in fact, it can save the union as long as the union is desirable from a social planner’s perspective. This means that the aggregate gains of the union are large enough and a regime with national currencies is not better for both countries.

Next, I will describe the setup and the exact mechanisms in detail. I set up a two-country open economy model following Corsetti and Pesenti (2005) and extend the framework to give governments the option to choose between being in a currency union and having an own national currency. With an own currency, the central bank -if credible- can focus on price stability and let the exchange rate float freely. In a currency union, there is only one central bank for both countries. The benefit of a common currency is that it facilitates cross-border flows, notably trade. By assumption, if both countries use the same currency, trade costs are reduced and bilateral trade increases, as in Alesina and Barro (2002). The downside of the currency union is that macroeconomic stabilization is less effective for certain states of the world since a common central bank sets interest rates for the whole union. Therefore, the costs of a currency union are time-varying and in some situations these costs might outweigh the benefits. I use this setup to run an experiment in which I calibrate the economy to simulate and then look at the outcome of four scenarios. In the first scenario, both governments decide freely when they want to leave the currency union. That is the only decision. They take monetary policy and the outside option as given. Once a government leaves the currency union, the union is destroyed forever. This gives rise to a limited commitment problem to the currency union itself as in Fuchs and Lippi (2006). In the second scenario, I add a union-wide Ramsey planner who sets lump-sum transfers between countries. The planner considers the member states’ exit option. The idea is to set transfers in such a way that no country takes benefit to leave the union. The aim is not to consider optimal fiscal policy that limits the costs of currency unions as in Dmitriev and Hoddenbagh (2019) or Schmitt-Grohé and Uribe (2016). Instead, I want to assess the minimum amount of transfers necessary to sustain the union. In the end, under the veil of ignorance, both countries are better off with this transfer scheme as the union survives. As in the first scenario, monetary policy is taken as given by the Ramsey planner. The third scenario considers a union-wide central bank that sets interest rates and takes the exit option of both countries into account. No transfers take place in this scenario. As before, the idea is to set interest rates in such a way that no country takes benefit to leave the union at any point in time. In the fourth and last scenario, I consider a joint monetary and fiscal response with a one-time monetary intervention in the crisis period itself and systematic transfers afterwards. All these four scenarios are run with different amounts of trade gains in a currency union that are consistent with the range of estimates from the literature. Considering a large set of trade gains also takes into account that leaving the union might imply other costs. For this note, I consider simulations with large trade gains of 6.5% increase in bilateral trade when joining the union and a situation with lower trade gains of 5%. The goal is to check which policy works depending on the amount of gains coming from the currency union. The paper has three main findings: First, I show how a central bank can prevent a break-up of the currency union by following an interest rule that puts more weight on stabilizing crisis countries that would otherwise exit the union. Second, I highlight that interest rate policy alone is a poor tool to redistribute between countries, as it depends on the synchronicity of business cycles. Compensation through interest rates is furthermore distortionary. Therefore – and this leads to the third result – the central bank alone can only sustain the union for some time, but if a sequence of sufficiently large asymmetric shocks emerges the union will eventually collapse. I demonstrate how fiscal transfers can sustain the union in the experiment in those situations in which interest rate setting alone cannot.

The first crucial result is the derivation of optimal monetary policy under exit options. Setting interest rates with participation constraints gives rise to a rule that features state-dependent country weights. When a country wants to leave the currency union, the central bank promises this country to put a greater emphasis on stabilizing its economy. This way the central bank makes the currency union relatively more attractive than the outside option with national currencies for the crisis country. Which country is stabilized more by the central bank is determined ex post, after shocks have materialized. Therefore, with the interest rate rule derived in this paper the central bank can in principle factor in exit options of member states.

To illustrate how a central bank can sustain a currency union when trade gains are large, I plotted in Figure 1 how interest rates evolve in a union without exit option (solid blue line), with exit options (dashed magenta line) and with a national currency (dotted red line). I have chosen a simulation where a large asymmetric shock occurs in period 37 (vertical green line). This large shock would lead to a breakup of the union under national planners. What happens in the crisis period is that the union-wide central bank alters its monetary stance and deviates from the solid blue line with equal Pareto weights. As H would exit the currency union without any intervention in this example, the central bank puts interest rates closer to what H would have chosen with an own currency. In addition to that, the central bank promises to keep the Pareto weight for H at the higher level until another participation constraint binds. This means that interest rates in future periods are systematically closer to what H would like to have. This is enough to put H at its participation constraint and to sustain the union.

Figure 1: Interest rates over time for one simulation with large trade gains (6.5% increase) of the currency union. The vertical green line indicates the time of a large asymmetric shock, where the Home country would leave the union.

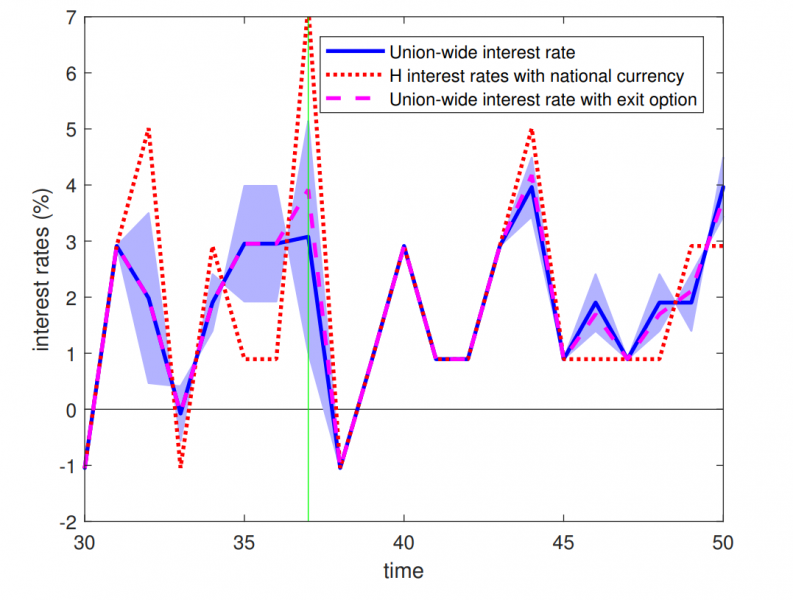
Two things are worth to highlight. First, as long as there is a currency union, the central bank is not able to replicate the allocation for the crisis country with national currencies by simply increasing/decreasing interest rates to the level they would have with national currencies. The reason for that is that the exchange rate is missing in a union. With national currencies and Producer Currency Pricing, interest rates can change without affecting production in the other country. The exchange rate movements ensure the shocks are absorbed. In a currency union, too low or too high interest rates will eventually hurt the other country’s production, which is bad for all members. Second, the central bank can only effectively favor a country and therefore redistribute in asymmetric states. In all symmetric states, the central bank can only implement one interest rate, as both countries want the same policy. Therefore, the central bank has to be more forceful in the asymmetric states. This leads to a strong increase in interest rates in the crisis period, from originally 3 % (the blue line) to 4% (the magenta line) that uses up almost half of the policy space available to the central bank, which is 5.2% as the maximum that can favor H in that example (the shaded blue are). This lack of policy space will be important for a scenario in which a currency union is less beneficial to start with. With large trade gains as in the example here, the central bank can sustain the currency union in all simulations until the end.

To illustrate that a central bank can sustain the union with large trade gains, Table 1 summarizes breakup probabilities for this scenario2. Break-up probabilities are computed by considering 2000 simulations of 100 years each. The algorithm checks, if the union has survived until the end of the simulation and -if the union collapses- when the collapse happens.

Table1: Break-up under different planners, trade gains 6.5%

Even in a simulation with high trade gains, a collapse of the union is rather likely within 100 years if no intervention happens (see the National Planner). The reason is that very large asymmetric shocks can happen within that considered time horizon, as those shocks are too costly for at least one country. Both fiscal and monetary policy are however enough to sustain the union and to accommodate the large asymmetric shock. When trade gains are lower, the potency of policy instruments changes: Now breakups would occur more frequently and monetary policy is not able to sustain the union forever, see Table 2.

Table 2: Break-up under different planners, trade gains 5%

As discussed before, the strength of monetary policy to redistribute and in turn to sustain the union is very limited which is the second key result of the paper. The central bank can only promise to favor a certain country in the future, if the business cycles of the member states are not perfectly synchronized. This means that a certain degree of asymmetry between both countries is needed for interest rates to be an effective tool. If business cycles are expected to be perfectly synchronized in the future, the central bank has no way to favor a specific country because both countries want to have the same interest rates. This puts a limit to the ability of the central bank to make promises to countries that are willing to leave, as compared to a planner who can promise transfers. This leads to the third result of the paper, namely that the currency union will eventually break up if monetary policy is the only tool considered to preserve the union. In the simulation, the central bank can increase the average duration of the currency union, but she cannot totally suppress the possibility of a break-up, see Table 2. With a monetary policy intervention, the union can be sustained for a while until a sequence of exceptionally large asymmetric shocks hit the union. I furthermore demonstrate in the experiment that fiscal transfers can sustain the currency union also in those simulations in which monetary policy alone fails to achieve that.

In conclusion, the central bank can help to sustain the union and reduce the probability of a break-up temporarily. This is done by partly departing from the original objective of union-wide price stability and emphasizing stabilization of crisis countries. The central bank however is only able to buy some time for the currency union. The option of using fiscal transfers is a more effective policy tool and ensures that the union is permanently sustained.