The Use of Trimmed-Mean Measures of Inflation in Monetary Policy Making: Differences between Old and New World Central Banks

Abtract

Some central banks publish data for trimmed-mean inflation calculated using higher-frequency price changes and make significant use of such measures in their monetary policy analyses, while others show data only for annual trimmed-mean inflation and make less use of such measures. Data for the United States, Canada and Australia provides strong evidence that monthly or quarterly measures of trimmed-mean inflation have significant information content about near-term inflation outcomes. Trimmed-mean measures can be viewed as having a much higher signal-to-noise ratio than headline CPI inflation. Central banks that are not calculating trimmed-mean inflation at the monthly (or quarterly) horizon are most likely passing up a clear opportunity to improve the information set available for monetary policy decision makers.

What are the Options for Dealing with the Noise in Monthly Inflation Data?

Many central banks focus on the annual rate of inflation in the analysis in their monetary policy reports. However, in a world where seasonal adjustment is relatively straightforward, there is much less reason than in the past to focus on annual changes in variables. Annual growth rates may be relatively smooth, but at the cost of being lagging indicators. Indeed, when the latest inflation data are published, 11/12ths of the annual inflation rate is already known. Barring revisions, the only news is in the latest one-month inflation rate. And changes in the annual rate tell us only how the most recent one-month inflation rate differs from the corresponding one-month inflation rate a full year ago.

If seasonal adjustment is effective, it becomes much more feasible to get information from one-month changes. Or three-month changes. Or perhaps the average of the most recent three months relative to the previous three-month period.

Perhaps not surprisingly, the recent sharp post-pandemic movements in inflation appear to have focused greater attention on shorter-horizon price changes and more recent data, including in some central banks that have traditionally focused more on annual changes. For example, the monetary policy reports of the central banks of Norway and Sweden have recently included graphs of domestic inflation that are similar to the left panel of Figure 1 below, which shows the equivalent series using the US CPI data. And a March 2023 speech by European Central Bank Executive Board member Philip Lane introduced the term ‘momentum indicator’ to describe three-month moving average inflation relative to the previous (non-overlapping) three-month period (Lane 2023).

Figure 1. Annualised US CPI inflation from price changes at different frequencies

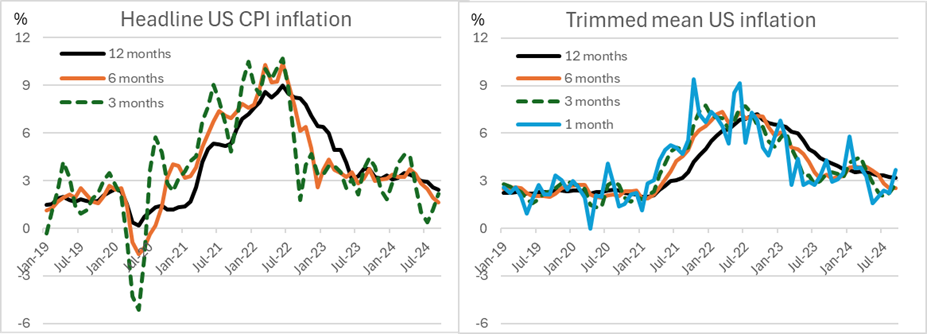
Sources: Author’s calculations based on data from Federal Reserve Bank of Cleveland

However, CPI inflation is more volatile when measured over shorter periods. And much of this volatility is likely to be ‘noise’ rather than ‘signal’. So as central banks make greater use of higher-frequency price changes, they frequently make use of measures of ‘underlying’ inflation, which can help to reduce noise and emphasise the signal. Wynne (2009) provides a useful overview of the history, and various interpretations, of the concept of underlying or core inflation.

Trimmed-mean measures of inflation are easily calculated and frequently used as indicators of underlying inflation. They capture the average rate of inflation after ‘trimming’ away some of the distribution of price changes at both ends of the distribution. Trimmed-mean measures downweight the impact of items if their price changes are unrepresentative in the period in question. This contrasts with ‘core’ or fixed-exclusion measures of inflation, which remove some prespecified items (typically food and energy) in every period, regardless of whether or not their price changes are extreme.

Different degrees of trimming are possible, but trims of 5-20 per cent from each end of the distribution are commonly used by central banks. The weighted-median rate of inflation is a special case of a trimmed mean, as it is the price change at the 50th percentile of the distribution of price changes.

Figure 2 shows monthly CPI inflation in the United States and Canada and illustrates how trimmed-mean measures are a straightforward way to significantly reduce the volatility in high-frequency inflation data.

Figure 2. Measures of Monthly CPI Inflation

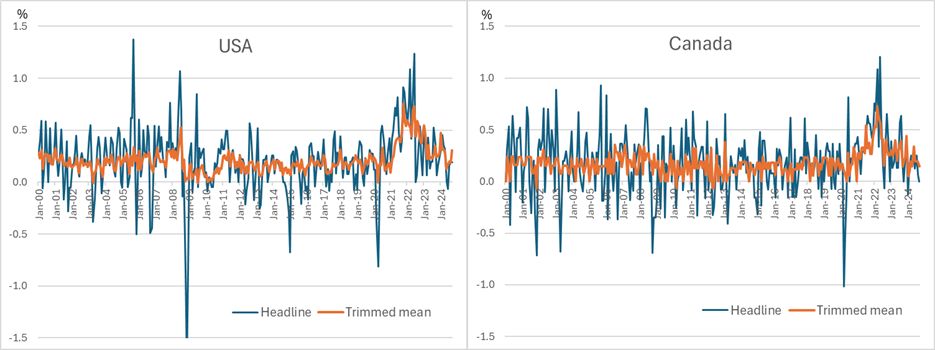
Sources: Federal Reserve Bank of Cleveland and Statistics Canada

We can also see the noise-reduction properties of trimmed-mean measures in the right panel of Figure 1. It shows annualised US trimmed-mean inflation from price changes at the same frequencies as in the left panel (3, 6 and 12 months) based on the Cleveland Fed’s 16 per cent trimmed mean, but it also adds annualised inflation based on just the most recent one-month trimmed-mean outcome. Note that the scales of the left and right panels are the same.

Figure 1 shows clearly that trimmed-mean measures of inflation calculated at all horizons are less volatile than the corresponding headline CPI inflation rate. And the gains in terms of reduced volatility are greatest at shorter horizons. Indeed, on some measures, annualised one-month trimmed-mean inflation is smoother than headline CPI inflation over 12 months!

The core thesis of Richards (2024) and this Policy Brief is that trimmed-mean inflation measures can be extremely useful indicators of the current underlying trend or momentum in inflation and can allow policymakers to make better use of the data in monthly inflation statistical releases.

How do Central Banks use Trimmed-Mean Inflation Measures?

A survey of the practices of nine advanced-economy central banks suggests some noticeable differences in the way that central banks publish and use measures of trimmed-mean inflation. In particular, there is an interesting divergence which might be described as an ‘old world’ versus ‘new world’ divide.

Central banks in the United States, Canada, Australia and New Zealand publish (or republish) data for trimmed-mean inflation calculated using price changes at the highest-available frequency (monthly for Canada and the United States, and quarterly for Australia and New Zealand) and make significant use of these measures in their monetary policy analysis. For Canada and Australia, trimmed-mean measures are the preferred indicators of underlying inflation.

In contrast, central banks in five other economies (the Euro Area, Norway, Sweden, Switzerland and the United Kingdom) make less use of trimmed means. Three of these (Norges Bank, Sweden’s Riksbank and the Swiss National Bank) regularly publish series for trimmed-mean inflation calculated at the annual frequency (using the distribution of annual price changes) but not at higher frequencies. The other two (the European Central Bank and the Bank of England) sometimes show data for annual trimmed-mean inflation in their published reports or refer to it in speeches by members of their decision-making bodies, but do not publish it on a regular basis.

While all of these European central banks refer to trimmed means as being part of the ‘suite’ of underlying measures used in their monetary policy analysis (see, e.g., Ehrmann et al, 2018), it appears that they do not take advantage of the benefits of trimmed means in reducing the noise in higher-frequency inflation data.

Evidence on the Performance of Trimmed Mean Inflation

There is now a significant amount of evidence from a number of countries from the past three decades, beginning with Bryan and Cecchetti’s (1993) work for the United States, that shows that measures of trimmed-mean inflation calculated using higher-frequency price changes are superior measures of underlying inflation to headline or ‘core’ measures. For example, Brischetto and Richards (2007) present results showing the benefits of trimmed-mean measures using data at the monthly frequency for the three largest advanced economies (the United States, the Euro Area and Japan) and at the quarterly frequency for Australia. And Lao and Steyn (2019) have recently shown that trimmed-mean measures perform well as measures of underlying inflation for Canada.

Richards (2024) presents some new evidence on the performance of trimmed means as measures of underlying inflation. The analysis uses data over a 30-year sample period beginning in 1994 for three countries – the United States, Canada and Australia – where the central bank or national statistical office publishes high-frequency (monthly or quarterly) trimmed-mean inflation calculated using seasonally-adjusted component-level price data.

A range of indicators – including the standard deviation and persistence of monthly or quarterly inflation rates, and the root mean squared error (RMSE) of these inflation rates relative to a 3-year centred moving-average rate – confirm that trimmed-mean measures of inflation are far less noisy than headline CPI inflation. On these measures, there is a 60-70 per cent reduction in noise in the monthly data for the United States and Canada. This is not surprising in light of Figure 2.

And trimmed-mean measures can also be useful in providing a guide to near-term inflation outcomes. Richards (2024) discusses in some detail the type of predictability that we might expect from a good measure of underlying inflation. In brief, I argue that assessments of the merits of different underlying measures should focus on the question of whether they contain information about future inflation at relatively short horizons – say over the next 3 6 months, rather than over the next 1-3 years as in some previous work.

There are two main reasons. First, I believe that shorter horizons correspond more closely to how central banks typically use their measures of underlying inflation. They use them as indicators of the current momentum in inflation and in forecasts of near-term inflation, whereas forecasts for inflation in the medium-term are determined by their structural models, which in turn reflect factors such as inflation expectations and forecasts for the output gap.

Second, the idea that the current level of underlying inflation should actually have significant explanatory power for inflation at a three-year horizon is puzzling. Importantly, inflation outcomes over the next 1-3 years will not only reflect conditions in the economy in the recent past, but will also reflect policy makers’ responses to those recent conditions. It is precisely because 1 3 years is the horizon that monetary policy has its most significant effect that we should not expect predictability of underlying measures at these horizons.

Accordingly, Richards (2024) examines how various measures of inflation over the previous 3 or 6 months (or 1 or 2 quarters) perform as naïve forecasts of inflation over the subsequent corresponding period. I also examine how they perform in regression (or Granger causality) tests of future inflation outcomes. Overall, the results suggest that recent trimmed-mean inflation outcomes have more information content for near-term inflation outcomes than recent outcomes for either headline CPI or ‘core’ inflation.

Finally, the paper contains some analysis of the relative benefits for naïve forecasts of CPI inflation of using data smoothing using time-averaging (e.g. using the annual rate of CPI inflation, which is the average of the past 12 monthly rates) versus smoothing based on cross-sectional information (e.g. using trimmed means which down-weight the effect of those items in the CPI basket with price changes that are unrepresentative in the period in question). Consistent with the information in Figure 1, the results of this exercise show very clearly that cross-sectional smoothing can dominate the use of time-series averaging, thereby allowing policy makers to focus more on the most recent data rather than the less timely information in annual price changes.

Conclusion

The main message of this work should be clear. It has confirmed some earlier findings that short-horizon measures of trimmed-mean inflation have significant information content for CPI inflation outcomes in the following half year or so – that is, they can improve near-term inflation forecasts. Trimmed-mean measures can be viewed as having a much higher signal-to-noise ratio than CPI inflation. They can provide policy makers – who are always ‘data dependent’ – with a clearer picture of the current momentum or trend in inflation, which is a key input into policy decisions. As the experience of recent years demonstrates, trends in inflation can change quickly, highlighting the need for policy makers to extract the best signal from the latest information available. The results suggest that trimmed-mean measures calculated at the monthly horizon are likely to warrant a leading place in any suite of high-frequency underlying inflation measures.

Overall, I conclude that central banks that are currently looking at trimmed-mean measures at only the annual frequency should be investigating the use of such measures based on monthly price changes to improve the information set available for monetary policy decision makers.