Uncertainty below the surface – what options tell us about the risks to bond yields and spreads

Abstract
In this policy brief, we show how option data can be used to gauge uncertainty around European government bond yields and detect the risk of large changes in sovereign spreads. Option-pricing reflects market expectations of future bond yields, which change over time. To capture these changes, we construct daily probability distributions of future government bond yields. Based on these, we describe two measures that provide insights into the tail risk to government bond yields, and the likelihood of significant spread movements. Due to their forward-looking characteristics, option prices are useful in predicting bond yields and spreads when benchmarking against backward-looking models. These enrich our toolbox for early warning signals and risk assessment. We provide some examples of their use from recent history.

Introduction

Anticipating changes in bond yields as well as movements of sovereign spreads represents an important challenge for economists, investors, and policy makers. Below the surface of directly observable benchmark government bond yields, markets also carry a wealth of information about expectations of future bond yields.  In particular, options reflect the range of expectations and show the market-implied probability of certain outcomes within a given time frame.  Option contracts can be seen as “bets” placed by market participants on the future price of the underlying asset. Investors might have different preferences, different information, or there could be disagreement about the expected state of the economy.

In a recent ESM working paper (Hudecz et al., 2024), we describe a methodology to derive option-implied probability distributions. We construct distributions of market-implied expectations 30, 45, 60, and 90 calendar days ahead for German, French and Italian governments bond yields, as well as for French and Italian spreads to Germany. These are informative not only with regard to the level of the expected sovereign yields and spreads between them, but also the uncertainty characterising these expectations. They also provide a gauge of bond yield and spread fluctuations that markets are prepared for in a given macroeconomic environment.

Furthermore, bond option pricing evolves over time, and the implied probability distributions change. We find that these changes in option-implied distributions correlate with global economic conditions, inflation expectations, monetary policy surprises, asset purchases, and stock market volatility. When comparing option-implied metrics to similar measures of uncertainty based on backward-looking models, we find the former to be more responsive than the latter to changes in economic conditions. Furthermore, their ability to predict both average and tail interest rate realisations is in most of the cases either comparable or higher than the one characterising backward-looking models. As new information comes in, investors change their views about the state of the economy, hence their expectations and preferences might be impacted.

The market-implied range of future bond yields widens when uncertainty is on the rise. In stress or uncertain environment, disagreement among market participants increases. The difference between the “bets” on higher and lower yields widens, the distribution becomes wider, and the tail risk increases. These distributions allow us to quantify the probability and magnitude of potential moves and can be used for risk assessment and early warning frameworks.

Methodology

There is a liquid market for option contracts on future prices of European government bonds, i.e. we observe each day market prices for the right to trade bonds at a range of prices at various future horizons. The Black-Scholes model allows us to derive the market implied volatility surface from option prices and we use the SABR model to interpolate between the volatilities at the discrete strike-prices. Next, as described by Breeden and Litzenberger (1978), we derive risk-neutral probability distributions, and we use linear interpolation to impute distributions at fixed horizons. We end up with market implied distributions as presented in figure 4, for any day since 2018, for any horizon up to 90 days ahead, for German, French or Italian 10-year bonds.

Furthermore, we are interested in the co-movement of the underlying bond yields i.e. the development of French-German and Italian-German bond yield spreads. We calibrate a student-t distributed copula on the historically observed co-movement and apply this copula to infer the bivariate distribution of market implied yield changes.

Applications

In our working paper, we derive several metrics for monitoring risks to sovereign debt markets. Here we give two examples that provide insights into the evolution of tail risks to government bond yields, and the likelihood of significant spread movements since 2018. First, we show the option-implied confidence bands around realised yields. Second, we show the probability of a change in spreads to be above a given threshold.

Following years of subdued volatility on bond markets, uncertainty started to rise in 2021. Figure 1 shows the realised 10-year German (Bund) and Italian (BTP) government bond yields, as well as the corresponding option-implied confidence bands around these central paths. As these figures show, the bands for Italy only are wide between 2018 and 2019, while for both countries these are relatively compressed between 2019 and 2021. Yet, the bands widened since the end of 2021, reaching the highest level in the fall of 2022. Although the wider distributions may be partly explained by higher realised bond yields, it still indicates the risk of larger jumps in terms of yield level.

Figure 1. Option implied confidence bands around government bond yields

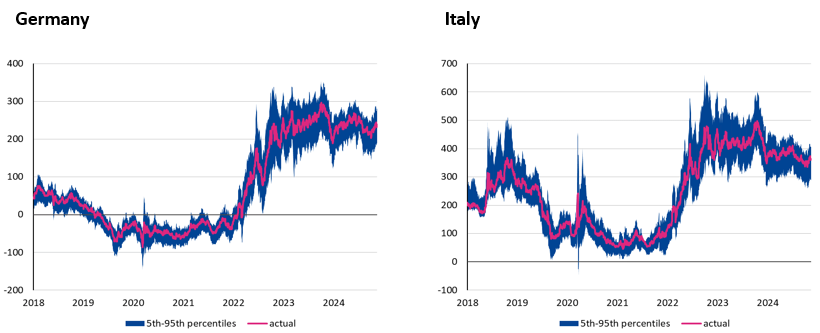
Source: Authors’ calculation based on Eurex and Bloomberg data. Note: The confidence bands refer to the 5 to 95 percentile range of yields 45 days ahead.

This market data is not only useful to analyse uncertainty in the past but also provides an outlook. While the previous charts focus on a constant horizon of 45 days over a long history, the fan chart in Figure 2 depicts the market expectation for German yields as of 12 November 2024, at different future horizons. As expected, the degree of uncertainty about yields increases, the longer the horizon, but particularly the speed of increase of tail risks as well as potential variation in skewness can inform scenario design at policy institutions.

Figure 2. Outlook of German yields on 12 November 2024

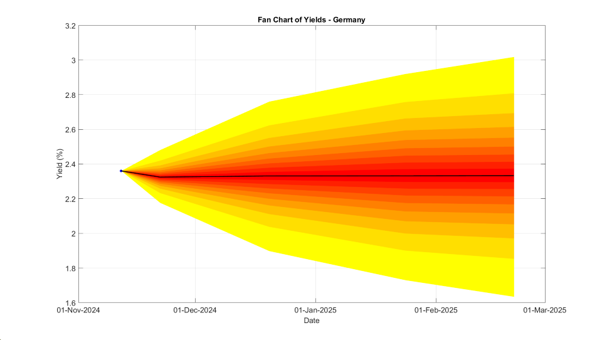
Source: Authors’ calculation based on Eurex and Bloomberg data. Note: The fan chart shades change in steps of 5 percentage points and are capped at the 5th and 95th percentile.

Other than looking at yields of single countries, we also assess the relative risk premium and construct distributions of the yield difference of two countries. In Figure 3 we depict the probability that the Italy-Germany spread will increase by more than 15 basis points over 45 days. This metric can be particularly insightful if applied in the context of early warning frameworks. Notable spikes in these probabilities were observed during specific events, such as the tumultuous government formation in Italy in 2018, the Covid-19 outbreak, and the energy crisis in the second half of 2022.

Figure 3. Probability of Italy-German spread increasing by 15 basis points

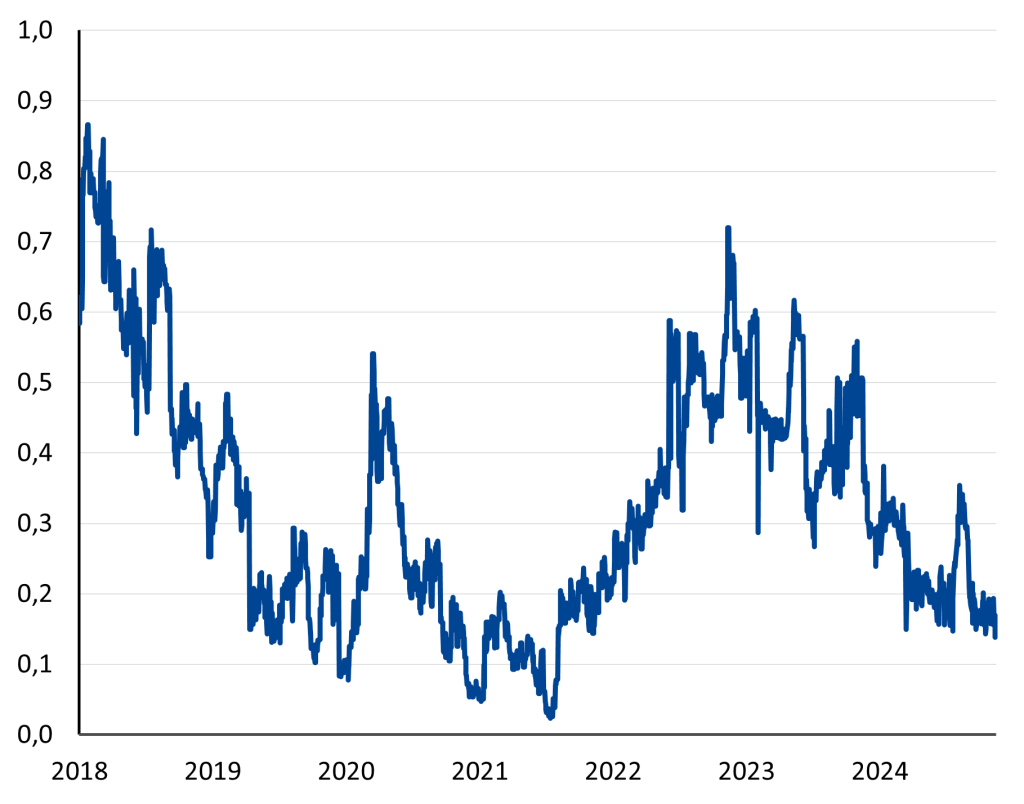
Source: Authors’ calculation based on Eurex and Bloomberg data.

The resent example of France

Figure 4 presents a specific recent example of the information embedded in option-implied densities, and their ability to reflect the probability and scale of changes in bond yields. It shows option-implied expectations of the 10-year French government bond yield 30 days ahead on three days surrounding political events that generated tensions on the French sovereign bond market over the last summer. The black dashed line refers to 3 June 2024 (i.e., one week before the European Parliament elections), the red solid line refers to 10 June 2024 (i.e., one day after the European Parliament elections), while the blue solid line depicts the distribution of expectations on 1 July (i.e., one day after the first round of the French legislative election).

When looking at changes characterising the peak and the shape of the distributions across the three days two main messages emerge. First, from 3 to 10 June, around the European Parliament elections, the distribution shifted to the right, and the mode moved from below 3% on 3 June, to roughly 3.2% one week later. This essentially captures the move visible in benchmark bond yields.

The second step reveals the subsequent increase in uncertainty, as reflected in bond options. Between 10 June and 3 July, around the first-round of the legislative election, the mode shift to the right was only marginal, but the distribution became much wider, signalling a substantial increase in uncertainty. The distribution also became skewed towards higher yields, as the right tail got heavier, which signalled that markets were pricing upside risks to the French yield as relatively more likely than downside risks. In other words, market participants were assigning a higher probability to further yield increases than to drops.

Figure 4. Option-implied distribution of 10-year French government bond yields

Source: Authors’ calculation based on Eurex and Bloomberg data.

Policy Implications

The above exercises allow us to gauge how the economic environment affects uncertainty on financial markets, and the pricing of possible outcomes. Even without dramatic changes in the underlying fundamental macro picture, markets are pricing a range of possible outcomes, and fluctuations in bond yields and spreads reflect this. Policymakers should be prepared to see market movements within these ranges, as these are anticipated and priced by markets.

Furthermore, sharp moves beyond these ranges, not yet priced by markets, can catch investors off guard and can be a major shock to bond markets. If the move takes place very rapidly and leaves no time for investors to adjust their positions, this can generate non-linear dynamics and raise the risk of “non-fundamental volatility” (Lane, 2020).

The market-based measures presented in this policy brief and discussed more in detail in Hudecz et al. (2024) could be used in further research addressing many questions within the empirical macro-finance literature.